Click on an image to go directly to a system or scroll to see the systems in this gallery.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| OdeFactory Images and Annotations | |
|
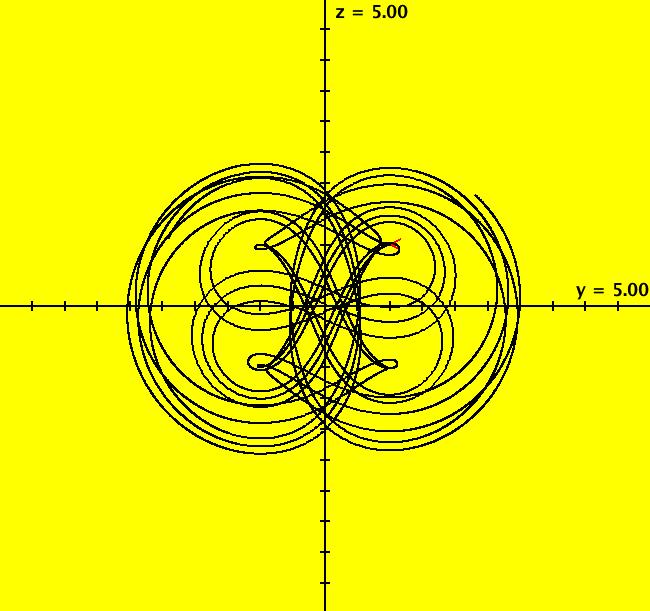
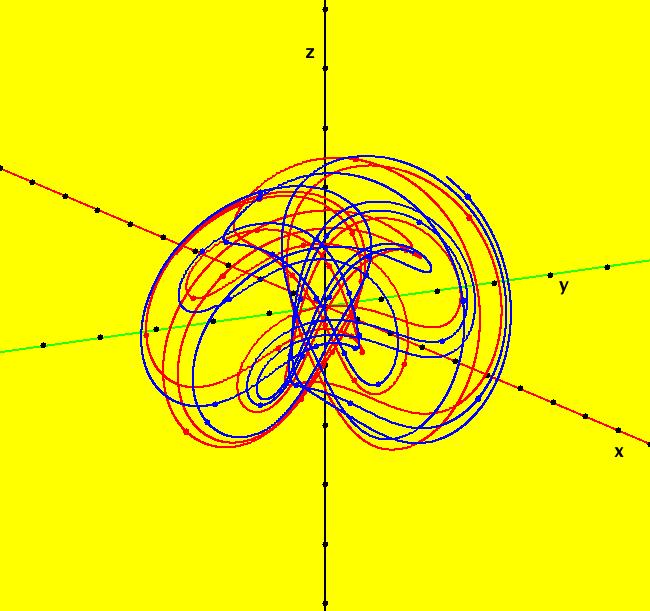
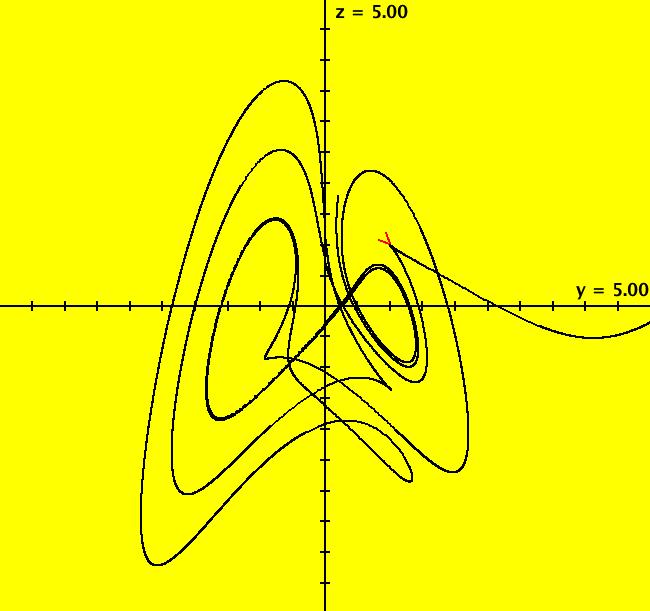
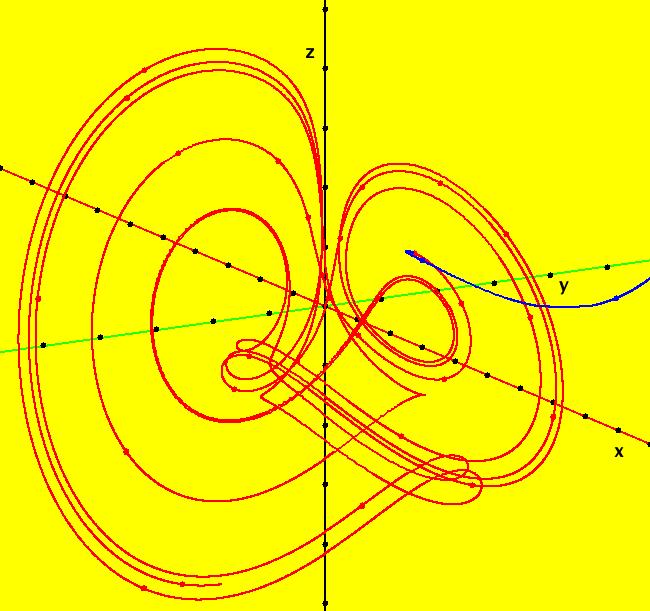
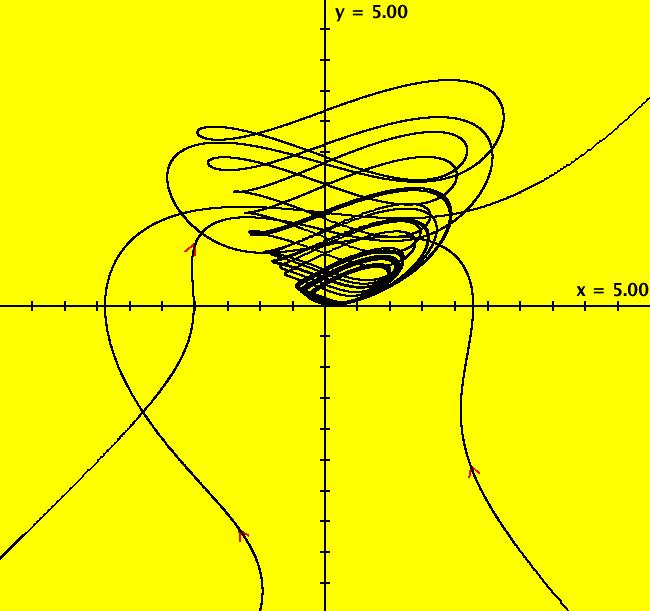
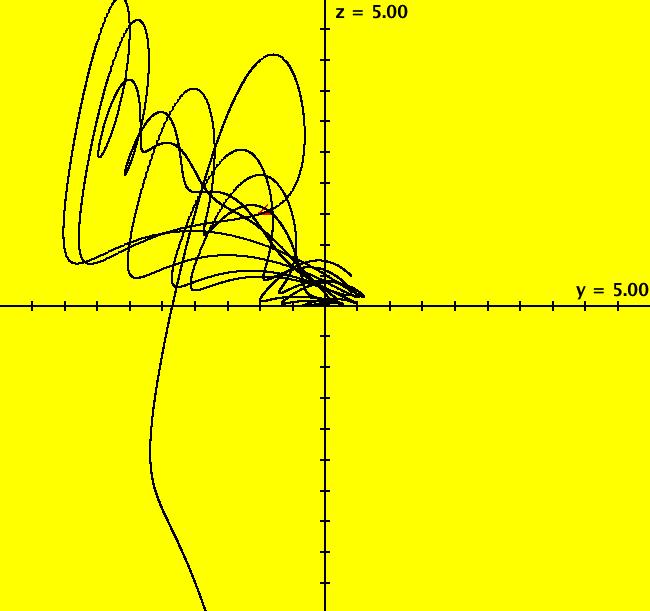
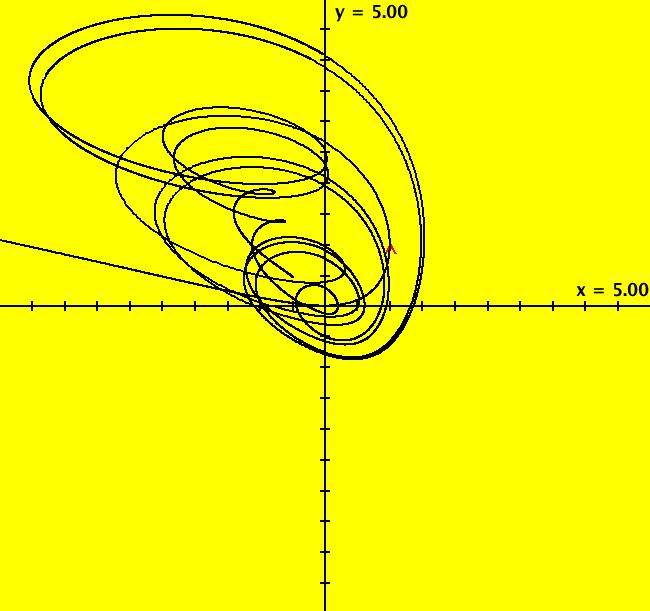
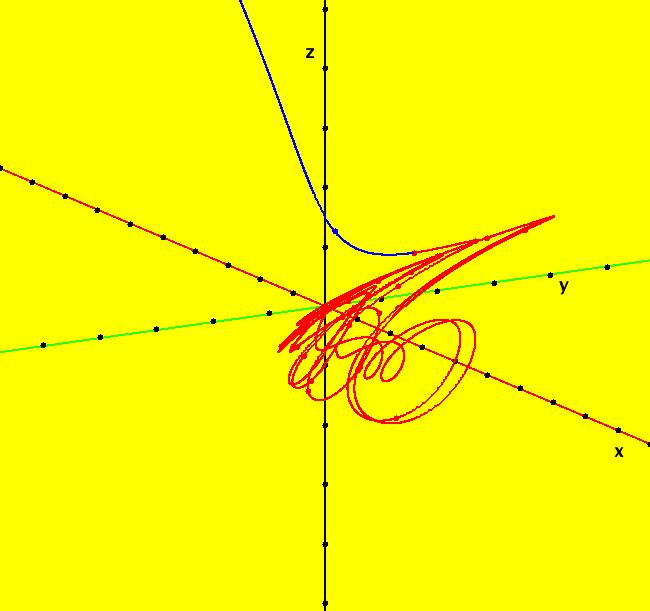
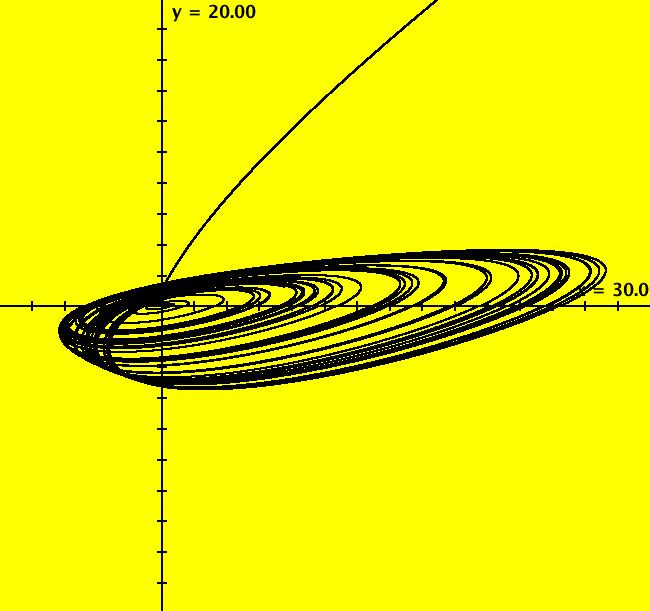
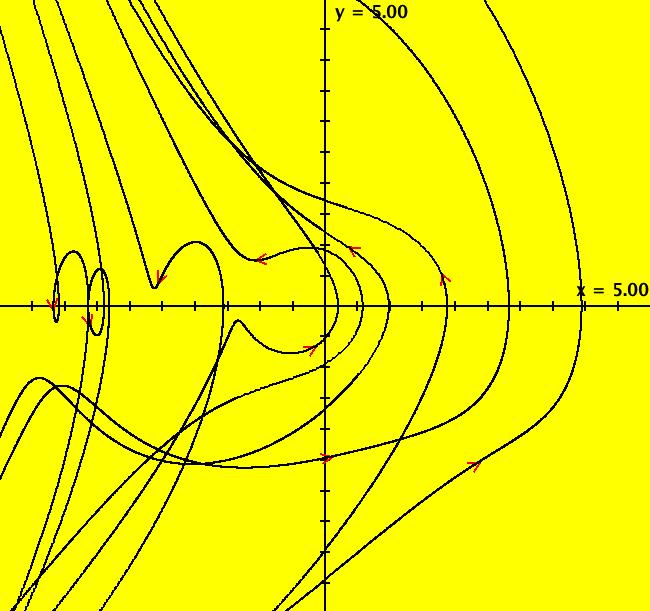
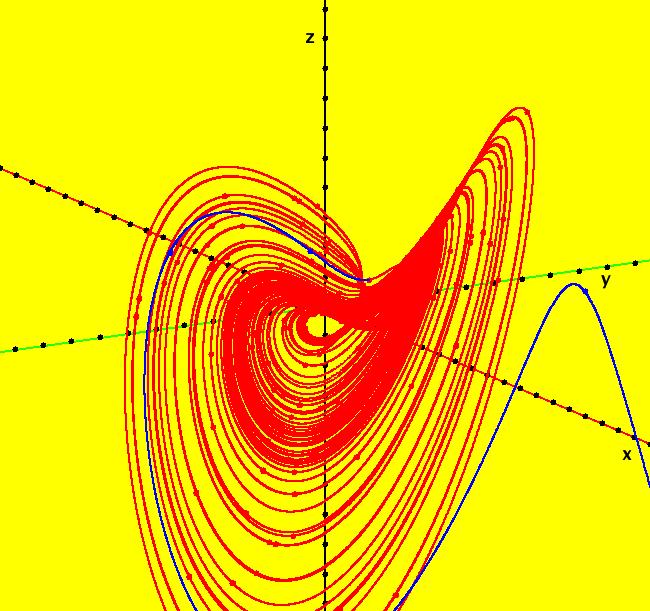
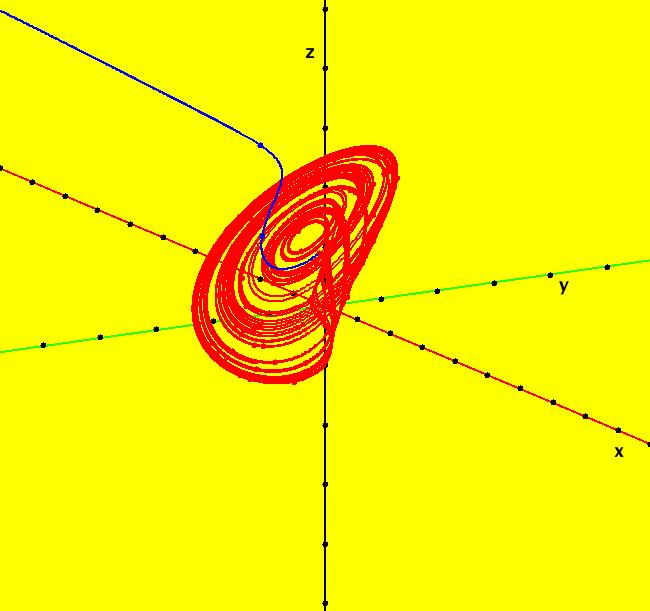
View/Sys/Gal: Ode "A: dx/dt = y, dy/dt = x-y*z, dz/dt = 1-y*y" in "Sprott'sChaoticFlows." The systems in this gallery are from: "Simple Chaotic Flow GIF Animations," by Prof. Sprott of the UW Madison Physics Department. You may also want to check out the lectire notes for Clint Sprott's Fall 2000 course: Physics 505, Chaos and Time-Series Analysis. Using OdeFactory you can modify and/or explore various features of the systems. The first system is: dx/dt = y, dy/dt = -x+y*z, dz/dt = 1-y*y The solution starts at x = 1, y = 1, z = 1 in the (y,z) view. If you want to start at a different point, use the "Clear" button then right-click in the viewing area. Select the (x,y,z) view, by selecting the x button in addition to the y and z buttons, to see the trajectory in the "3D" phase space. To return to the (y,z) view, deselect the x button. In the (y,z) view, to see an animation of the flow, click the "Flow..." button. Increase the speed and/or duration as needed. If you make changes to the system, you can get back to the original version by selecting it from the list of systems in the gallery. If you want to save your new version, select "Add to Gallery" on the "Gallery" menu and give the system a new name. For help using OdeFactory select "OdeFactory User Guide" on the Help menu. Image 1: Ode (y,z) view. Image 2: Ode (x,y,z) view.
|
|
|
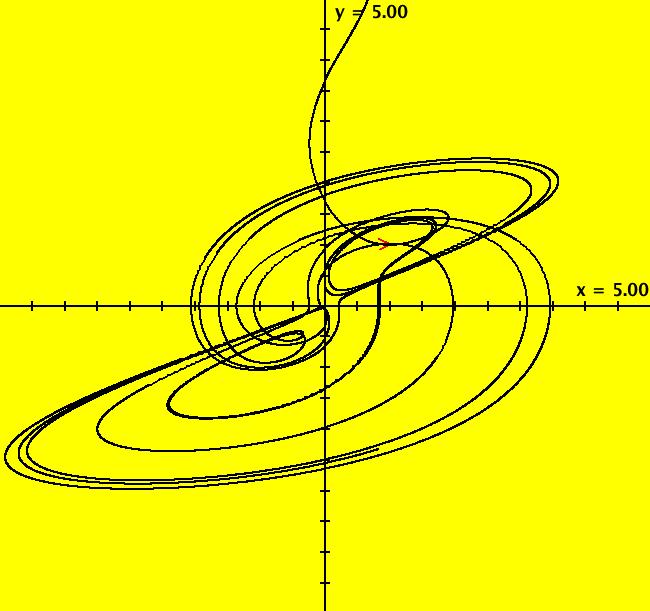
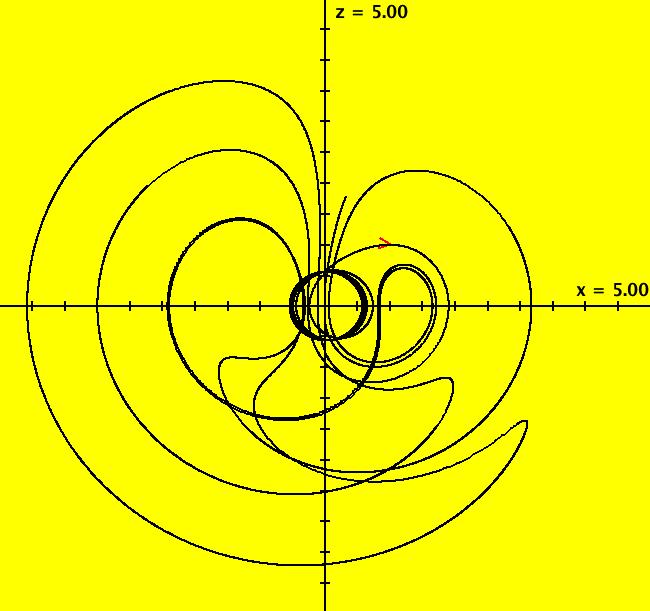
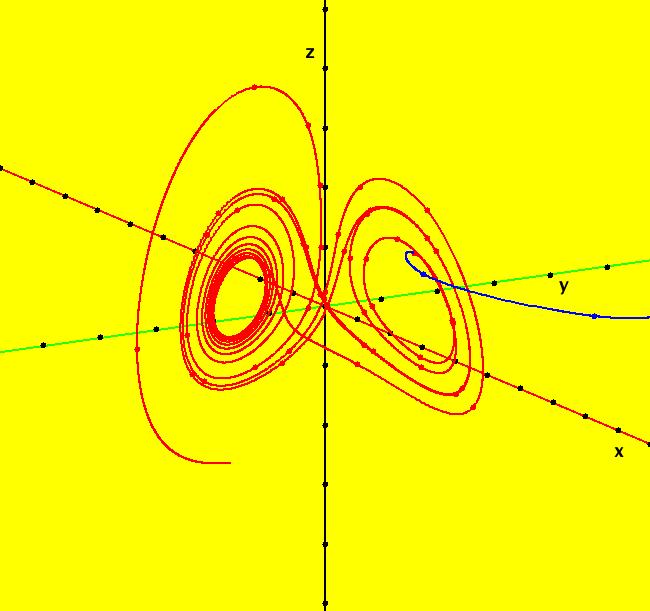
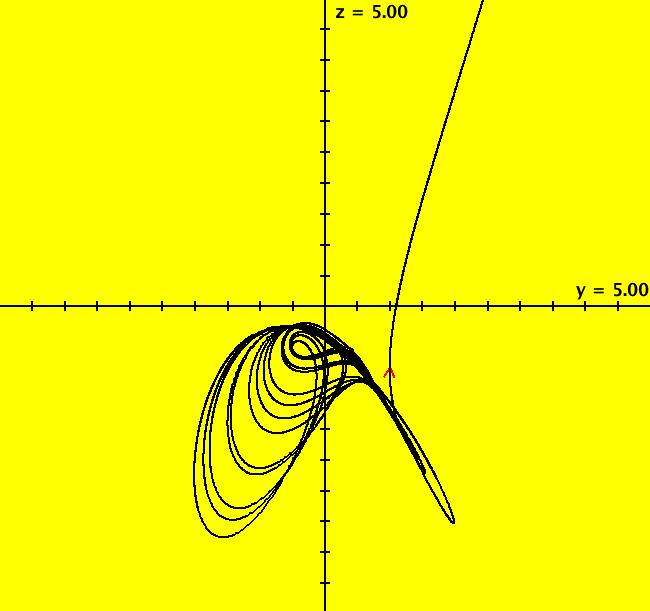
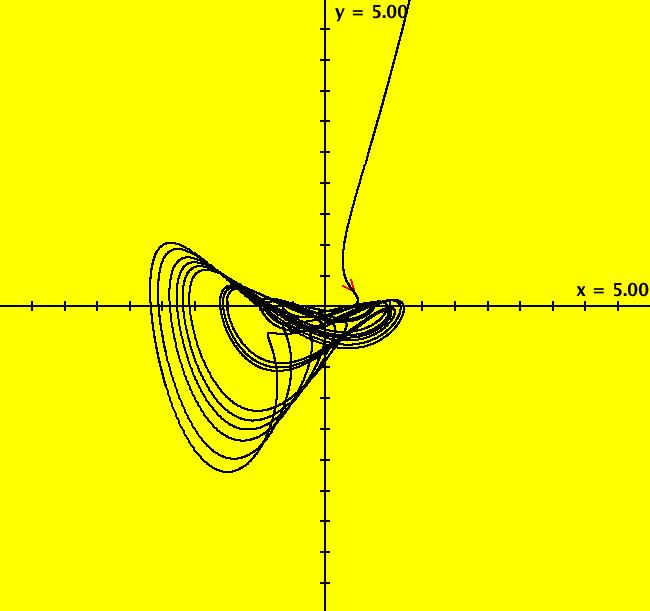
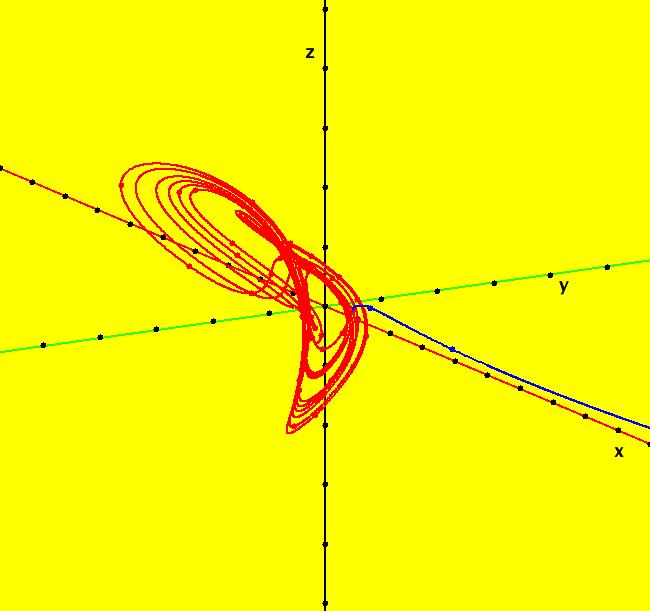
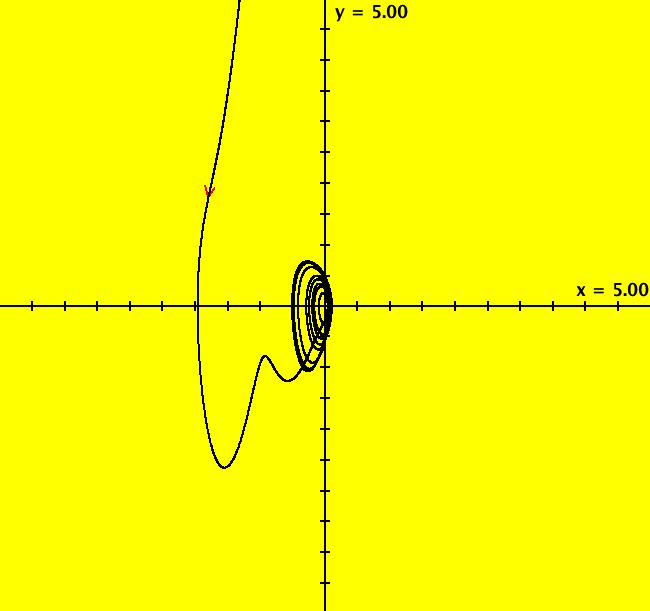
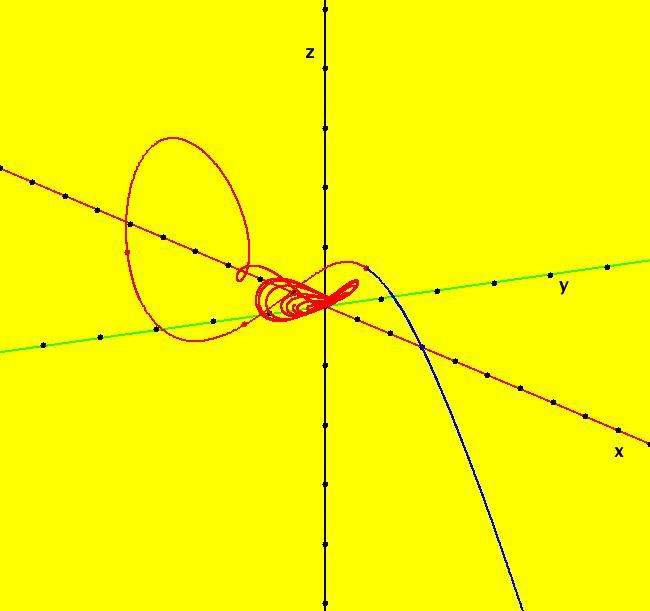
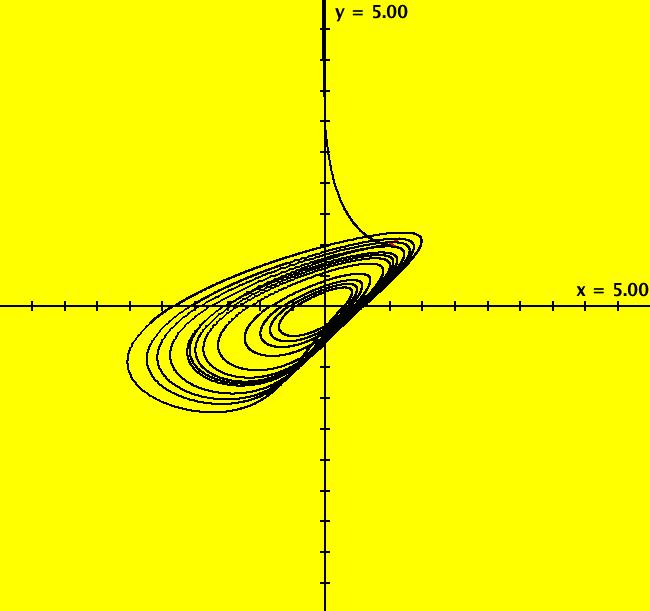
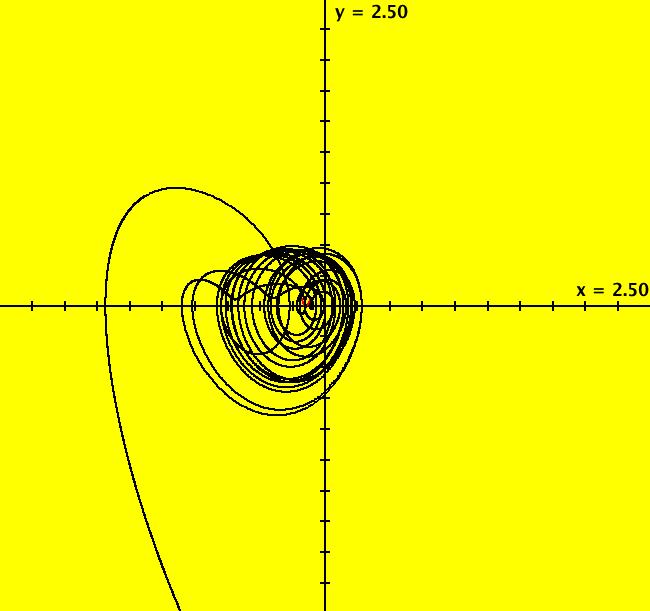
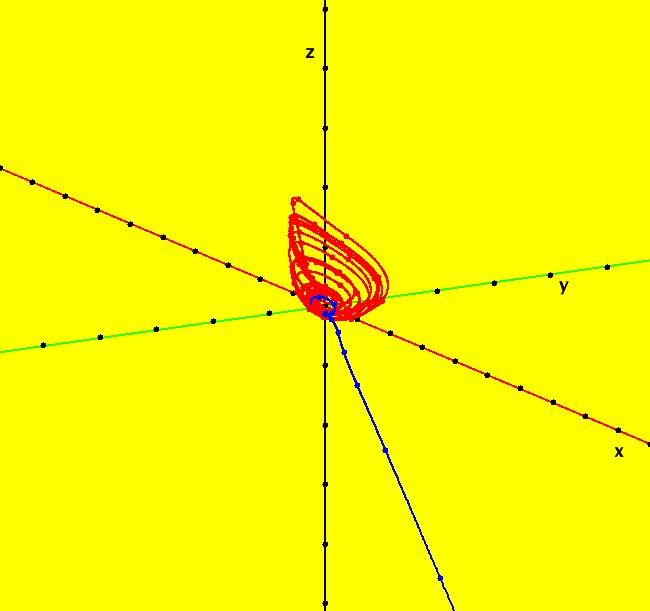
View/Sys/Gal: Ode "B: dx/dt = y*z, dy/dt = x-y, dz/dt = 1-x*y" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = y*z, dy/dt = x-y, dz/dt = 1-x*y Solutions starts at x = 1, y = 1 and z = 1 in the (x,y), (x,z) and (y,z) views. Image 1: Ode (x,y) view. Image 2: Ode (x,z) view. Image 3: Ode (y,z) view. Image 4: Ode (x,y,z) view. You can start an animation in any of these views. Set the speed of the dot to Max and the duration of the animation to 60 seconds.
|
|
|
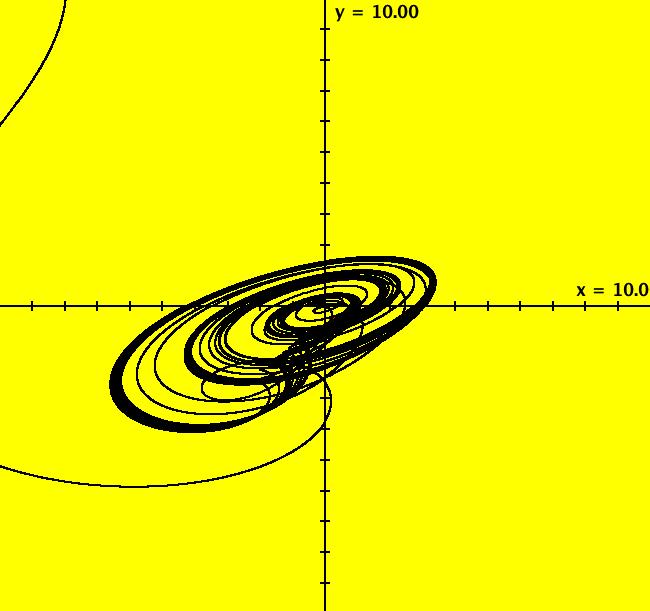
View/Sys/Gal: Ode "C: dx/dt = y*z, dy/dt = x-y, dz/dt = 1-x*x" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = y*z, dy/dt = x-y, dz/dt = 1-x*x The solution starts at x = y = z = 1 in the (y,z) view. Select the (x,y,z) view to see the trajectory in the "3D" phase space. Image 1: Ode (x,y,z) view. To see an animation, select the (y,z) view and click the "Flow" button.
|
|
|
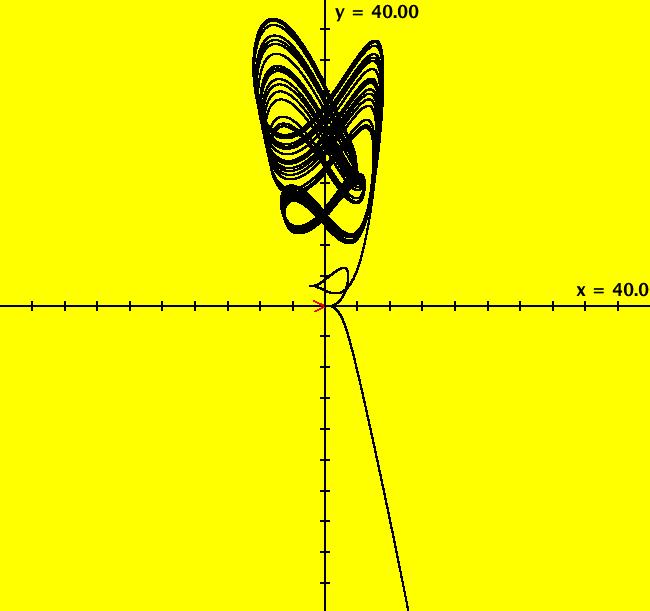
View/Sys/Gal: Ode "D: dx/dt = -y, dy/dt = x+z, dz/dt = x*z+3*y*y" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = -y, dy/dt = x+z, dz/dt = x*z+3*y*y
The solution starts at x = 1, y = 1, z = -1 in the (y,z) view. Image 1: Ode (y,z) view. Run an animation in -t. Check the "3D" view by selecting all three x, y and z buttons. Toggle the x button to return to the (y,z) view.
|
|
|
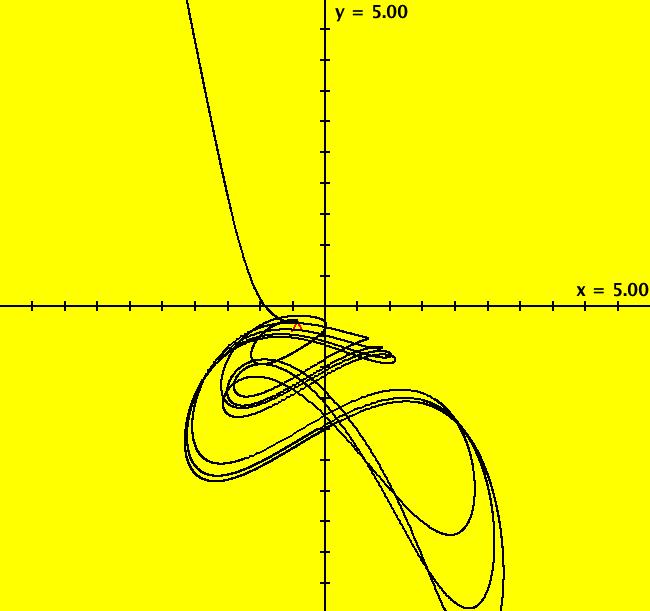
View/Sys/Gal: Ode "E: dx/dt = y*z, dy/dt = x*x-y, dz/dt = 1-4*x" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = y*z, dy/dt = x*x-y, dz/dt = 1-4*x The solution starts at x = -2, y = 1, z = 1. It was extended in +t by clicking on the arrow head. The lower trajectory with ICs (x,y,z) = (-1.319018,-3.630470,1.000000) does not go to the attractor. Image 1: Ode (x,y) view. Try an animation. Try the "3D" view.
|
|
|
View/Sys/Gal: Ode "F: dx/dt = y+z, dy/dt = -x+0.5*y, dz/dt = x*x-z" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = y+z, dy/dt = -x+0.5*y, dz/dt = x*x-z The solution starts at x = 1, y = -1, z = 1.5 in the (y,z) view. Click on the arrowhead at (y,z) = (-1,1.5), get into the 3D view, then extend the solution curve in +t. Image 1: Ode (y,z) view.
|
|
|
View/Sys/Gal: Ode "G: dx/dt = .4*x+z, dy/dt = x*z-y, dz/dt = -x+y" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = 0.4*x+z, dy/dt = x*z-y, dz/dt = -x+y. Image 1: Ode (x,y) view. Image 2: Ode (x,y,z) view.
|
|
|
View/Sys/Gal: Ode "H: dx/dt = -y+z*z, dy/dt = x+0.5*y, dz/dt = x-z" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = -y+z*z, dy/dt = x+0.5*y, dz/dt = x-z Image 1: Ode (x,y) view. Image 2: Ode (x,y,z) view.
|
|
|
View/Sys/Gal: Ode "I: dx/dt = -0.2*y, dy/dt = x+z, dz/dt = x+y*y-z" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = -0.2*y, dy/dt = x+z, dz/dt = x+y*y-z Image 1: Ode (x,y,z) view. Image 2: Ode (x,y,z) view.
|
|
|
View/Sys/Gal: Ode "J: dx/dt = 2*z, dy/dt = -2*y+z, dz/dt = -x+y+y*y" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = 2*z, dy/dt = -2*y+z, dz/dt = -x+y+y*y Image 1: Ode (x,y) view.
|
|
|
View/Sys/Gal: Ode "K: dx/dt = x*y-z, dy/dt = x-y, dz/dt = x+0.3*z" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = x*y-z, dy/dt = x-y, dz/dt = x+0.3*z Image 1: Ode (x,y) view.
|
|
|
View/Sys/Gal: Ode "L: dx/dt = y+3.9*z, dy/dt = 0.9*x*x-y, dz/dt = 1-x" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = y+3.9*z, dy/dt = 0.9*x*x-y, dz/dt = 1-x Image 1: Ode (x,y) view.
|
|
|
View/Sys/Gal: Ode "M: dx/dt = -z, dy/dt = -x*x-y, dz/dt = 1.7+1.7*x+y" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = -z, dy/dt = -x*x-y, dz/dt = 1.7+1.7*x+y Image 1: Ode (x,y) view.
|
|
|
View/Sys/Gal: Ode "N: dx/dt = -2*y, dy/dt = x+z*z, dz/dt = 1+y-2*x" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = -2*y, dy/dt = x+z*z, dz/dt = 1+y-2*x This system may not have a chaotic attractor or it might just be hard to find. Image 1: Ode (x,y) view.
|
|
|
View/Sys/Gal: Ode "O: dx/dt = y, dy/dt = x-z, dz/dt = x+x*z+2.7*y" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = y, dy/dt = x-z, dz/dt = x+x*z+2.7*y Image 1: Ode (x,y) view.
|
|
|
View/Sys/Gal: Ode "P: dx/dt = 2.7*y+z, dy/dt = -x+y*y, dz/dt = x+y" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = 2.7*y+z, dy/dt = -x+y*y, dz/dt = x+y Image 1: Ode (x,y,z) view.
|
|
|
View/Sys/Gal: Ode "Q: dx/dt = -z, dy/dt = x-y, dz/dt = 3.1*x+y*y+0.5*z" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = -z, dy/dt = x-y, dz/dt = 3.1*x+y*y+0.5*z Image 1: Ode (x,y) view.
|
|
|
View/Sys/Gal: Ode "R: dx/dt = 0.9-y, dy/dt = 0.4+z, dz/dt = x*y-z" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = 0.9-y, dy/dt = 0.4+z, dz/dt = x*y-z Image 1: Ode (x,y,z) view.
|
|
|
View/Sys/Gal: Ode "S: dx/dt = -x-4*y, dy/dt = x+z*z, dz/dt = 1+x" in "Sprott'sChaoticFlows." This system of odes is defined by the equations: dx/dt = -x-4*y, dy/dt = x+z*z, dz/dt = 1+x Image 1: Ode (x,y,z) view.
|
|