Click on an image to go directly to a system or scroll to see all of the systems in this gallery.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| OdeFactory Images and Annotations | |
|
An OdeFactory Slide Show Click on a slide to zoom in. Click "video" to see a video. |
View/Sys/Gal: Ode " Overview" in "SeparatrixExs." Separatrices are trajectories that partition the phase space into components in which all trajectories are topological equivalent. Separatrices are most often studied in the context of 2D systems. For a 1D system, the phase space is just the real line. If the system is autonomous, the "separatrices" are just the fixed point solutions and the "components" are just the line segments between the fixed points. 1D systems can always be rewritten as geometrically equivalent 2D systems in that the solution curves in the extended phase space of the 1D system are the same as the trajectories in the phase space of the 2D system. The 2D system, corresponding to the 1D system dx/dt = f(t,x) is just dx/dt = 1, dy/dt = f(x,y). It is best to study the "separatrices" of 1D systems by studying the separatrices of the corresponding 2D system.
|
|
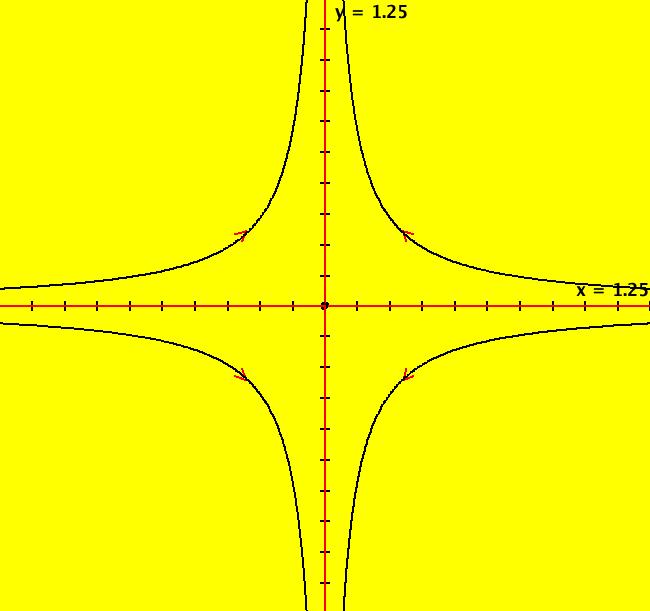
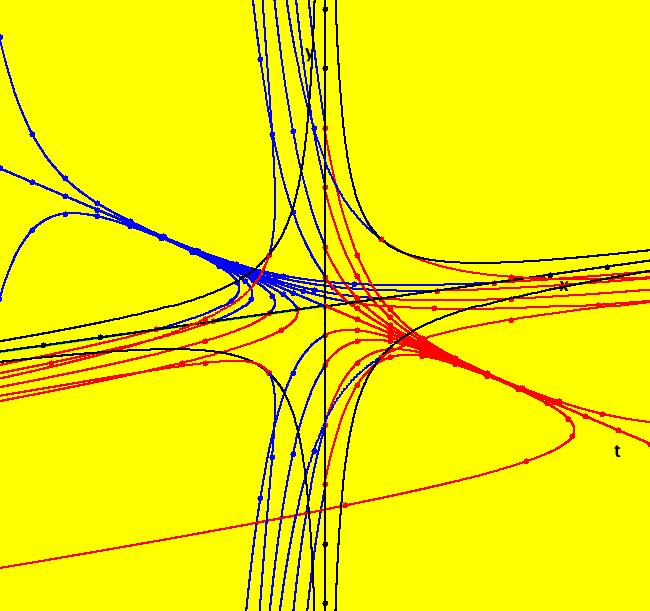
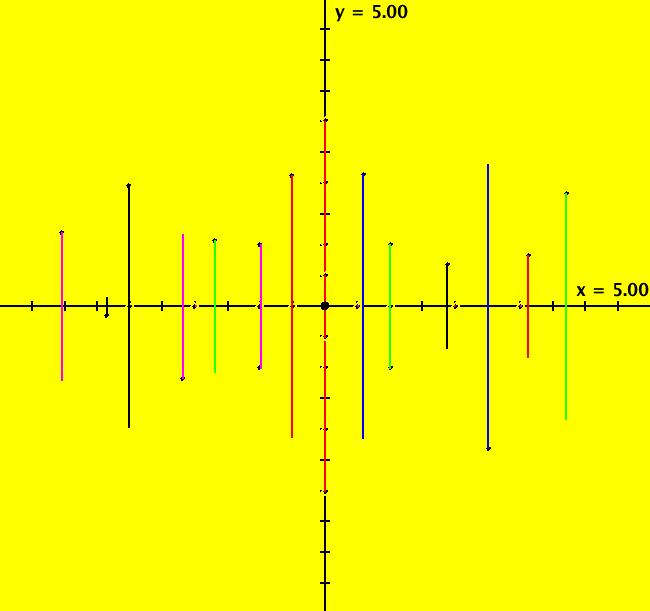
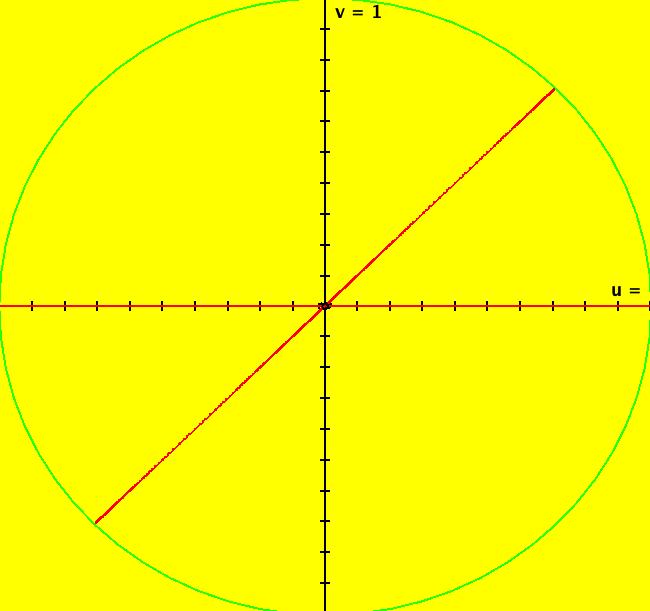
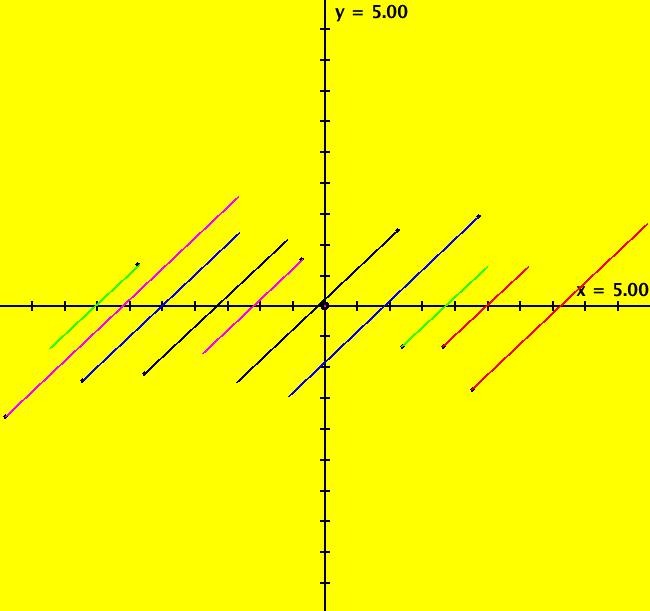
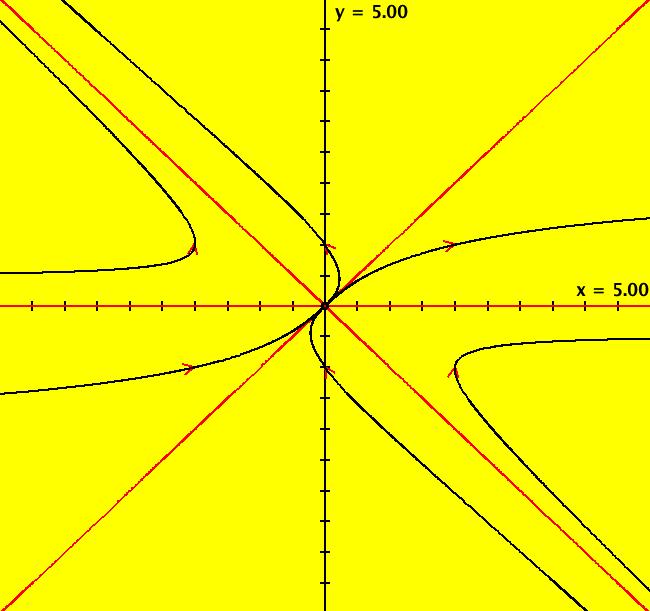
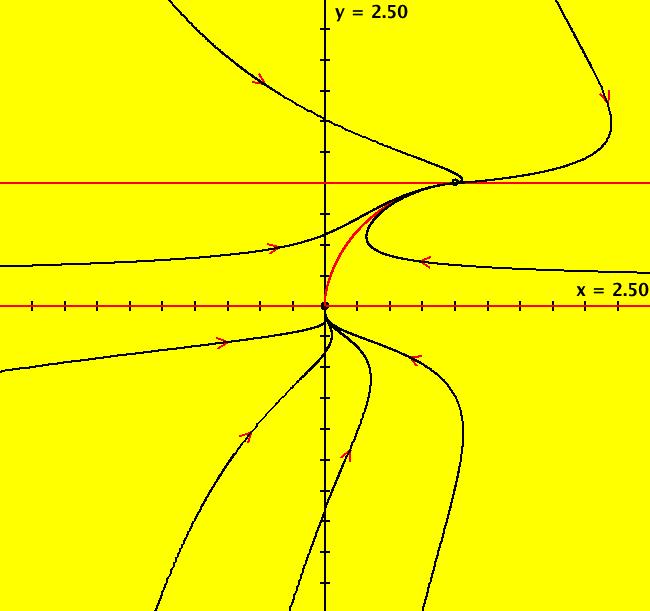
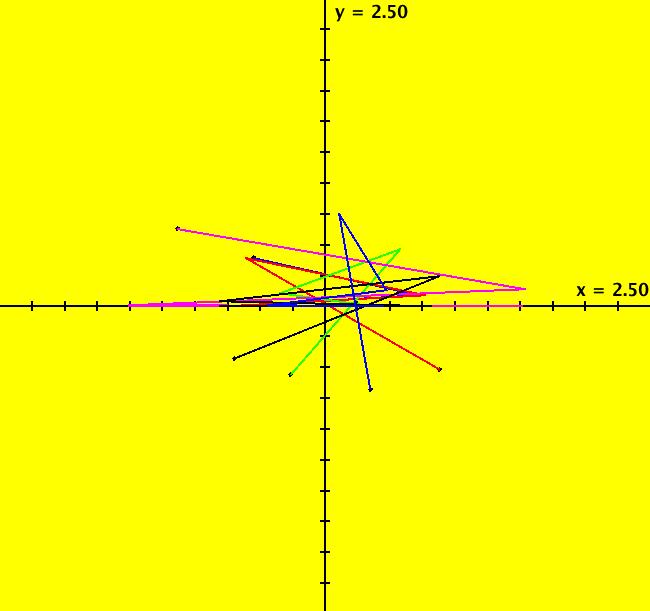
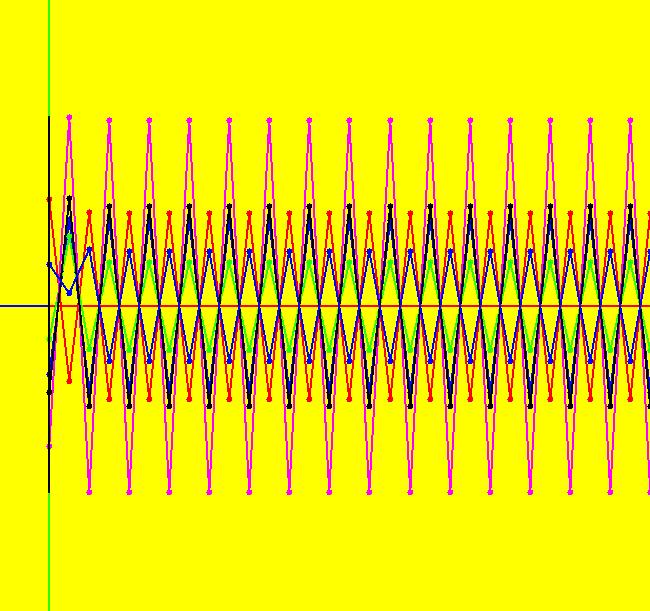
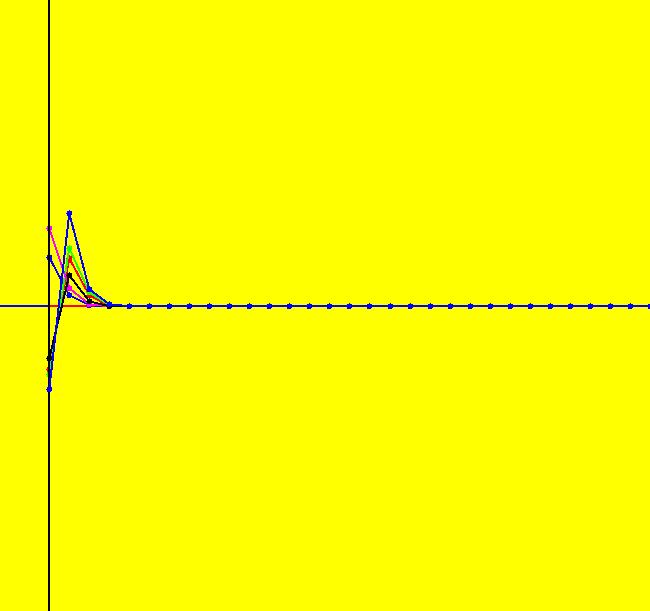
View/Sys/Gal: Ode "2D: 1, linear: (-x,y), drawing a global phase portrait" in "SeparatrixExs." *************** 1/1/17 ***************** The 2D systems in this gallery have been updated to include a discussion of IMap separatrix systems. For an introduction to IMap separatrix systems, see gallery IMapSeparatrixExs. **************************************** This system of odes is defined by the equations: dx/dt = -x, dy/dt = y A global phase portrait contains all there is to know, qualitatively, about a 2D system. It is best constructed in the R2 view then shown in the R2+ view. --> See the discussion of the Poincare compactification mapping of R2 to R2+ in the OdeFactory User Guide. --> To draw the global phase portrait for the system: (a) in the R2 view, look for saddle points using the vector field or by simply starting several random trajectories, (b) next, find the fixed point at each saddle point (by inspection or by using WA) and start a fixed point solution at the saddle point, (c) partition the phase space into components by starting two approximate separatrix trajectories "in the saddles" near each saddle point, (d) finally start a representative trajectory in each component. All trajectories in each component are topologically equivalent while trajectories in different components are topologically distinct. --> Try a Flow animation in R2+ and notice the fixed points at infinity. Aside: the system is a Hamiltonian system with H(x,y) = -x*y = c, so dx/dt = Hy = -x, dy/dt = -Hx = y. Setting c = 0 gives solutions x = 0 and y = 0 which are the separatrix curves. The general solution is the family of hyperbolas y = -c/x. The sectors near the fixed point at (0,0) are called "hyperbolic" sectors. Image 1: The Ode separatrix system consists of the x and y axes. IMap orbits, except for the fixed point at (0,0), are all per-2, parallel to the x axis and symmetric about the y axis. The IMap separatrix system is just the point (0,0). Image 2: Some IMap orbits.
|
|
|
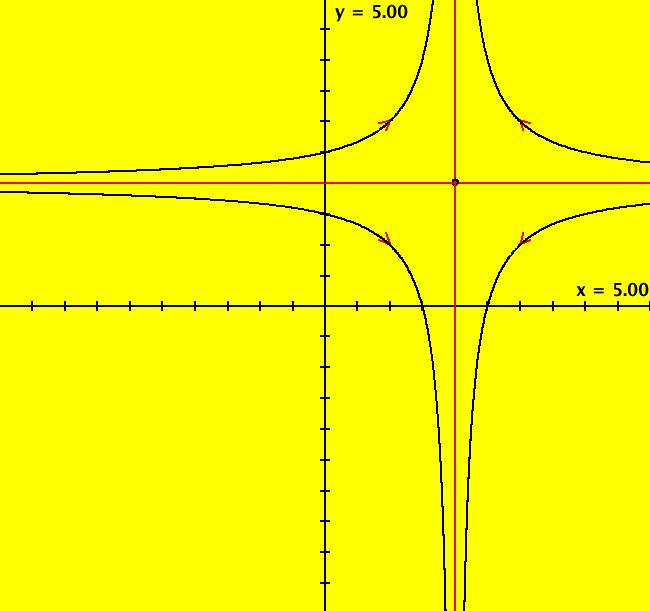
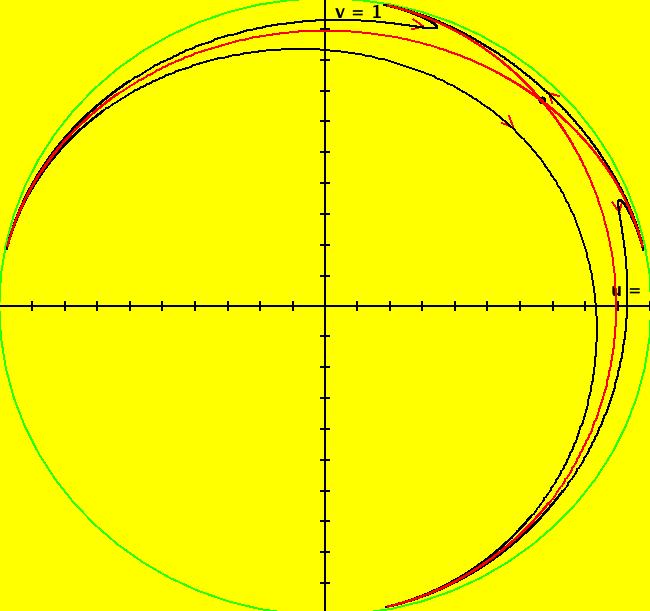
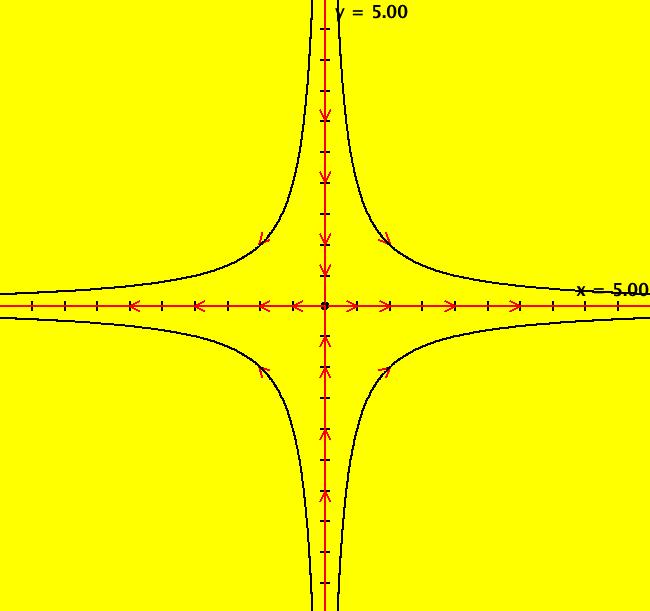
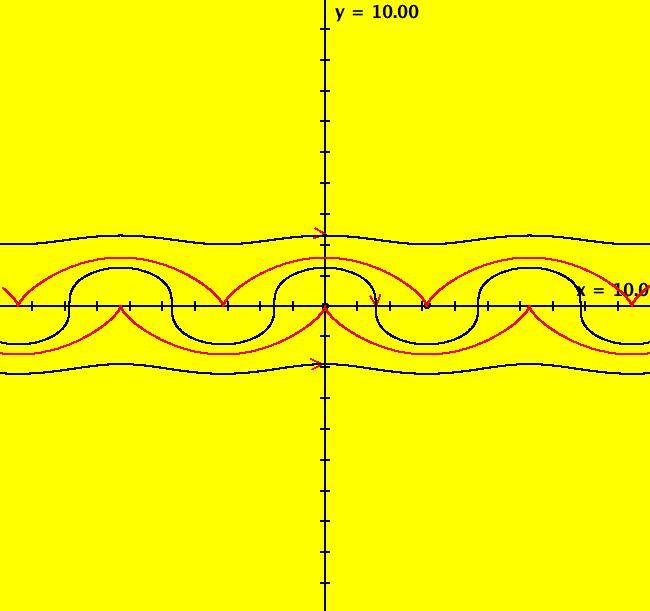
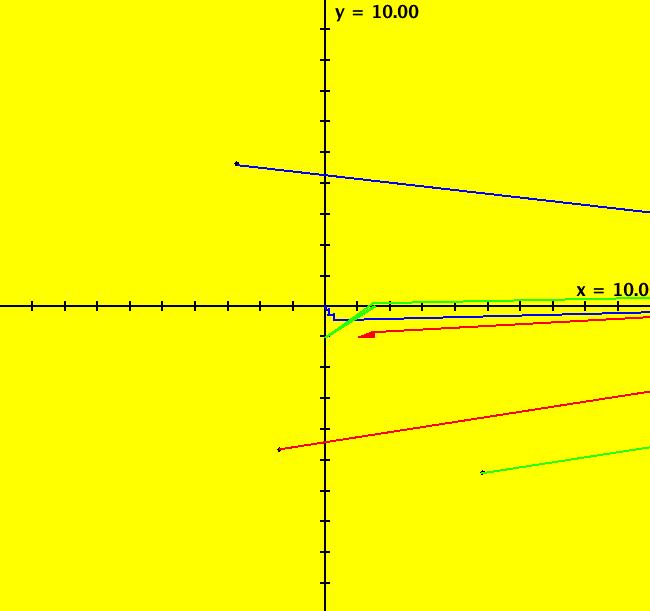
View/Sys/Gal: Ode "2D: 2, linear: (-(x-2),(y-2)), saddle not at (0,0)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = -(x-2), dy/dt = (y-2) To draw the phase portrait shown... (a) clear (b) fixed point: start a traj at (2,2) (c) separatrices: start trajs at (2.0001,2.0001) and (1.9999,1.9999) (d) start trajs at (1,3), (3,3), (1,1) and (3,1) Image 1: The Ode separatrix system in the (x,y) plane. Image 2: The Ode separatrix system in the R2+ view. Image 3: An EMap view w/CT 9. All IMap orbits go to infinity except the fixed point orbit at (1,1) so the IMap separatrix system is just the point (1,1).
|
|
|
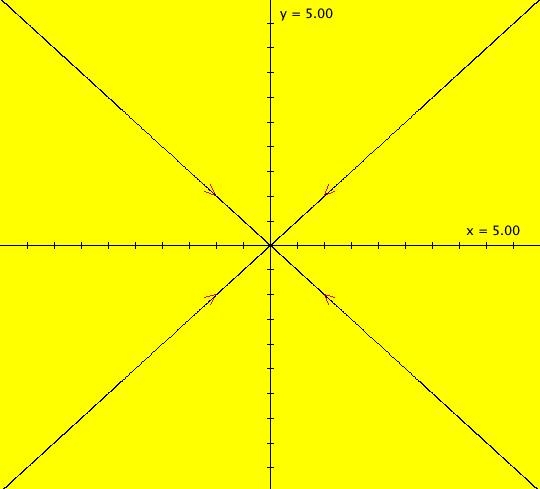
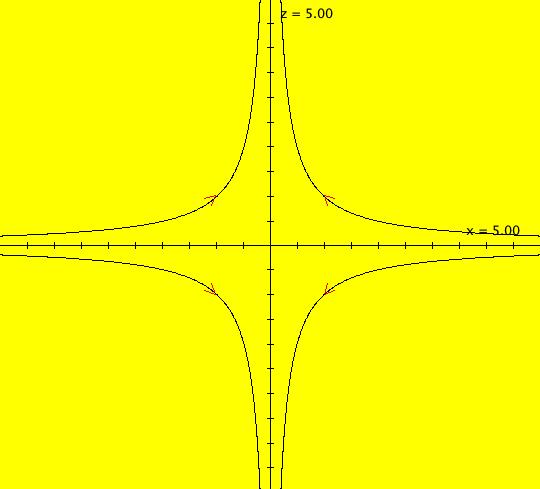
View/Sys/Gal: Ode "2D: 3, linear: (x,-y)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = x, dy/dt = -y The Ode separatrices are the four trajectories consisting of the half-lines: y = 0, x > 0, y = 0, x < 0, x = 0, y > 0 and x = 0, y < 0. The fixed point is the trajectory consisting of the single point: x = 0, y = 0. Every trajectory consisting of more than one point defines a 2D surface in the extended phase space parallel to the t axis. Image 1: The Ode phase space view. Image 2: The Ode extended phase space, 3D/(t,x,y), view. All IMap orbits, with seeds not on the x axis, have per-2 with points at (x,y) and (x,-y). The IMap separatrix is the x axis. Image 3: IMap orbits.
|
|
|
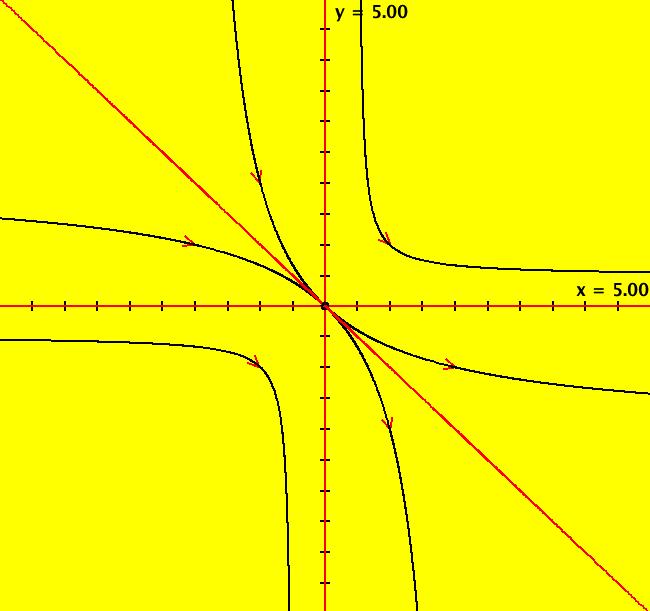
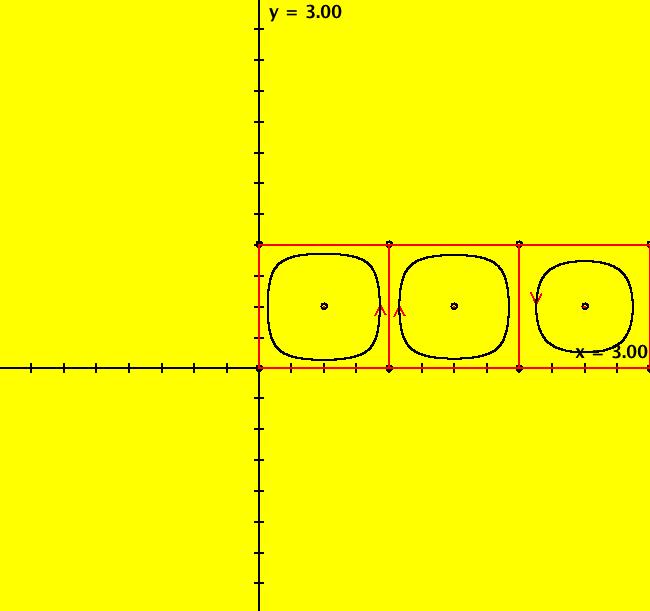
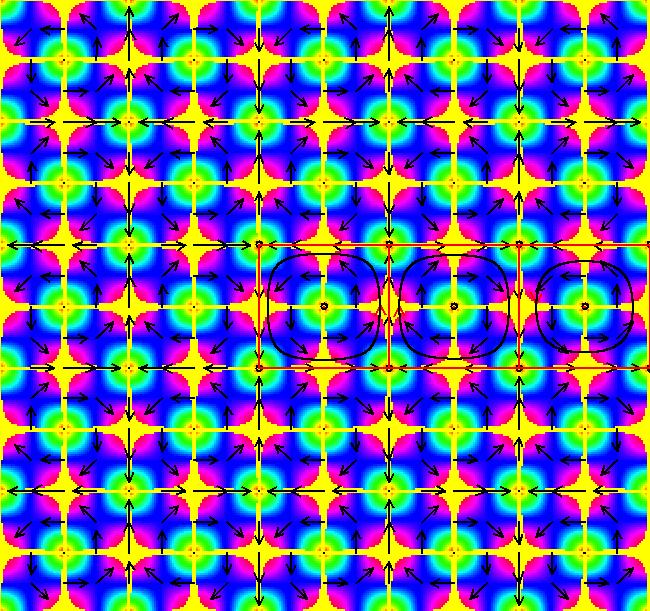
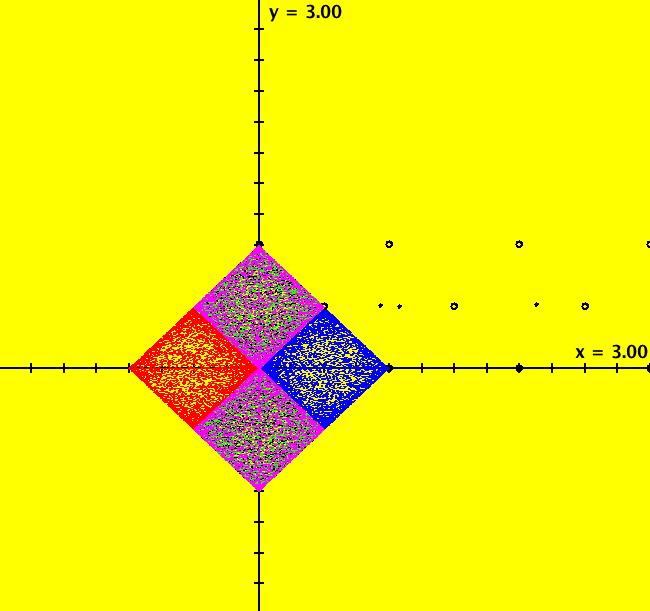
View/Sys/Gal: Ode "2D: 4, linear: (x-2*y,-y), wiggle method" in "SeparatrixExs." Approximate Separatrix ~~~~~~~~~~~~~~~~~~~~~~ This system of odes is defined by the equations: dx/dt = x-2*y, dy/dt = -y To start an approximate separatrix in OdeFactory near the saddle point, (0,0), either: (a) shift wiggle at (0,0) or (b) start trajectories close to (0,0) at (.01,.001) and (-.01,-.001). Approximate separatrices are drawn in red by OdeFactory. For this simple linear example, the separatrices are obviously the lines y = x and y = 0 so we could simply start trajectories on the separatrices. However, in nonlinear cases we cannot find exact points on separatrices so we are forced to start trajectories near the fixed point to draw approximate separatrices. When a 2D system can be linearized at a saddle point, the straight lines through the fixed point in the directions of the eigenvectors of the linearized system provide good starting points for approximate separatrices. --> Click on (0,0) to see the ICs for the trajectories starting near (0,0). --> Zoom in to see the ICs for the trajectories starting near (0,0). Image 1: Ode separatrix system in the R2+ view. All Ode trajectories, except for the fixed point at (0,0), go to infinity but IMap orbits not. All Ode trajectories, except for the fixed point at (0,0), go to infinity but IMap orbits not. All IMap orbits for y ≠ 0 are per-2 with points (x,y) and (x-2*y,-y). The x axis, which is the IMap separatrix, consista of fixed points. Image 2: The IMap view.
|
|
|
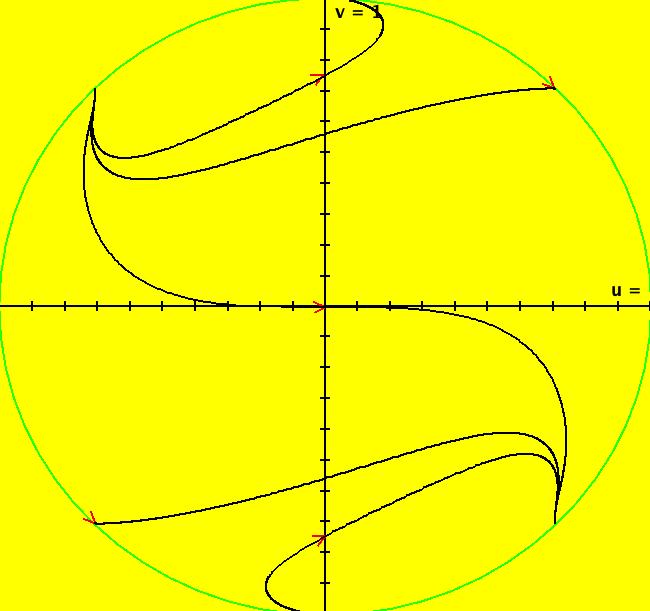
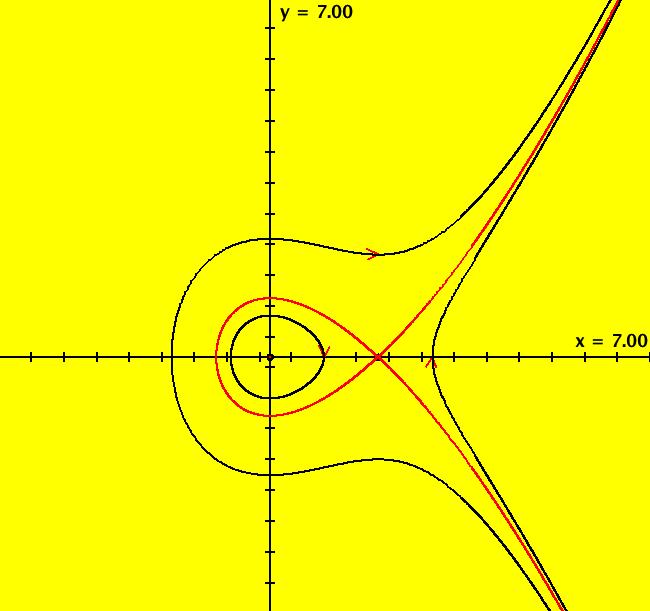
View/Sys/Gal: Ode "2D: 5, poly deg2: (x^2-t^2) -> (1,y^2-x^2)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = 1, dy/dt = y^2-x^2. It is a 2D corresponding to the 1D system dx/dt = x^2-t^2. There are no finite fixed points however there are six fixed points at infinity given by: (u,v) = (0,+-1), sqrt(2)(+-1,+-1). Trajectories starting at (10,10) and (-10,-10) are approximate separatrices. The global phase space has three components. Image 1: The global phase Ode portrait in the R2+ view. No finite fixed points but fixed points at infinity (see R2+ view). All trajectories starting below the upper "V" -> the right half of the lower "V" in +t. All trajectories starting above the lower "V" -> the left half of the upper "V" in -t. Image 2: The EMapMax view. The boundaries of the prisoner set are the IMap separatrices. All bounded IMap orbits go to a per-2 limit cycle between (1,-1) and (1,0).
|
|
|
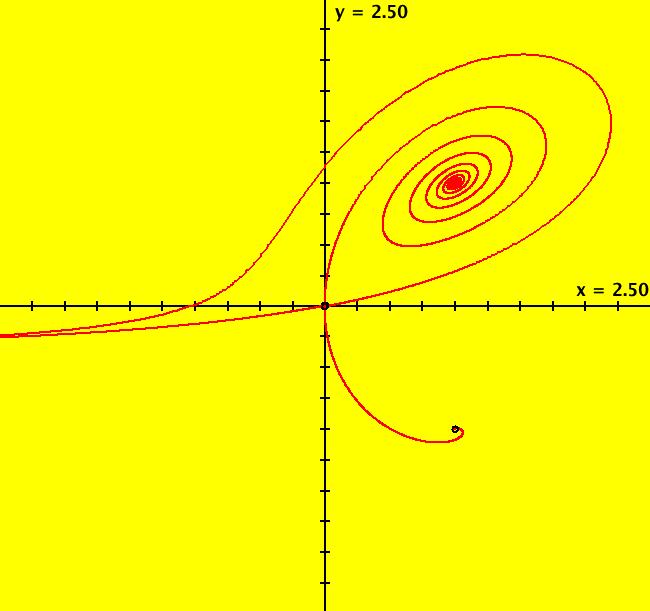
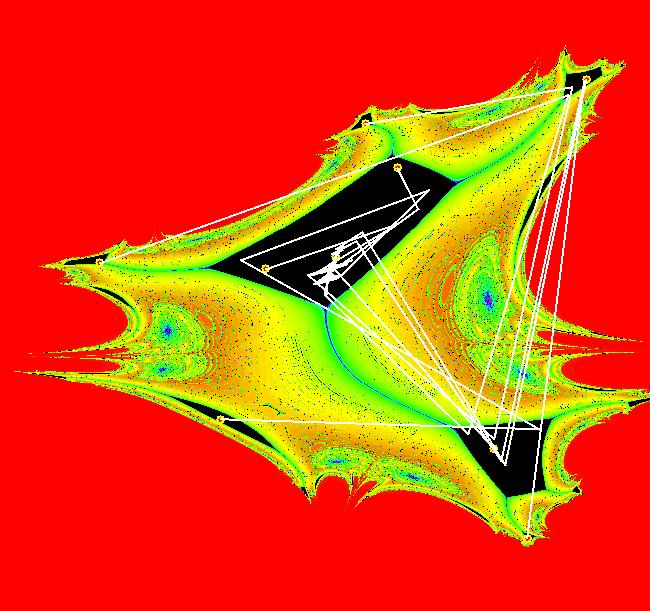
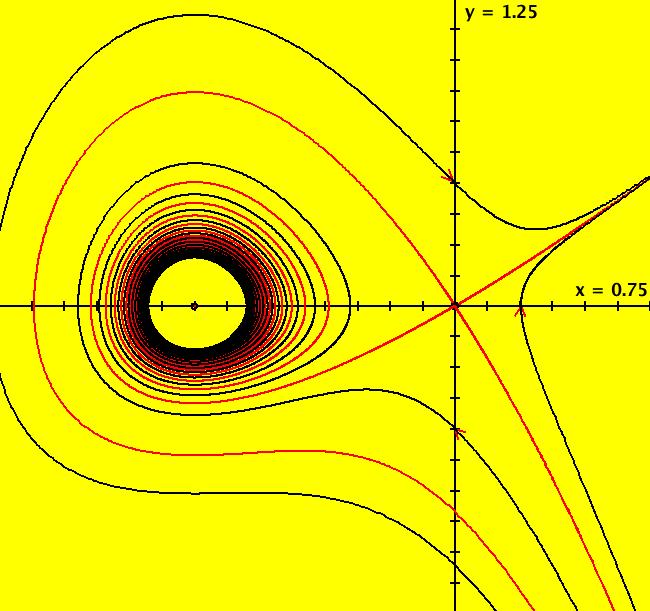
View/Sys/Gal: Ode "2D: 6, poly deg2: (-x+y^2,-a*x+y+a*y^2-x*y), a = .4; " in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = -x+y^2, dy/dt = -a*x+y+a*y^2-x*y Parameters are: a = .4; ICs are: (.001,.001), (-.001,-.001), (1,-1). Image 1: The Ode separatrix system for a = .4. The Ode has fixed points at (0,0) and (1,-1). This system is also interesting in the IMap view and in the and EMap view w/CT 0. Image 2: The EMapMax view. The boundaries of the prisoner sets form the IMap separatrix system. All bounded IMap orbits go to fixed point (.08,.4). In the Ode, IMap and EMap views, adjust "a" to see what happens.
|
|
|
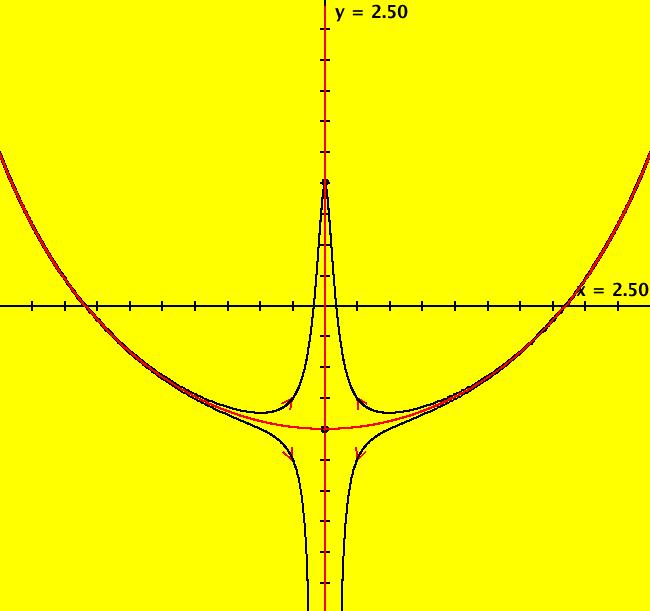
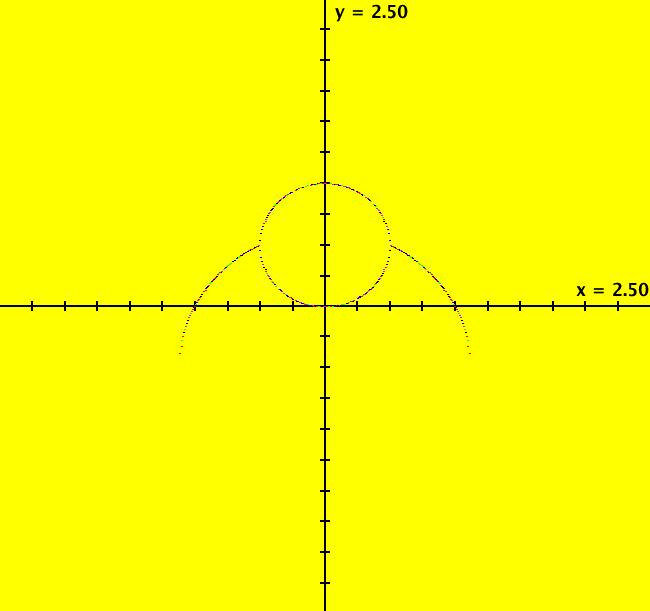
View/Sys/Gal: Ode "2D: 7, poly deg2: (-x,1-x^2-y^2)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = -x, dy/dt = 1-x^2-y^2 Ode fixed points are at (x,y) = (0,+-1) and (u,v) = (0,+-1). (0,-1) is a saddle point. ICs are: (-.0001,-.9999), (.0001,-1.0001), (0,1.0001), (+-.25,-1.25), (+-.25,-.75) Approximate Ode separatrices are in red. Image 1: The Ode's separatrix system. Image 2: In the EMap view, the IMap's separatrix system is the boundary of the prisoner set. All bounded IMap orbits go to per-2 limit cycles. Image 3: The IMap view with a 500+ seeds in the EMap prisoner set. Only the last points on the per-2 limit cycles are shown. The points are on the circle centered at (0,.5) of radius .5 and the curves off the right and left sides of the circle.
|
|
|
View/Sys/Gal: Ode "2D: 8, poly deg2: y=x, y=-x, x=0 are separatrices" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = x^2+sqrt(2)*x*y-y^2, dy/dt = sqrt(2)*y^2 The lines y = +-x and y = 0 are separatrices. Zoom in to see the ICs near (0,0). Image 1: The Ode separatrices. Image 2: EMap view. The IMap separatrix system is the boundary of the prisoner set. All orbits starting in the prisoner set go to (0,0).
|
|
|
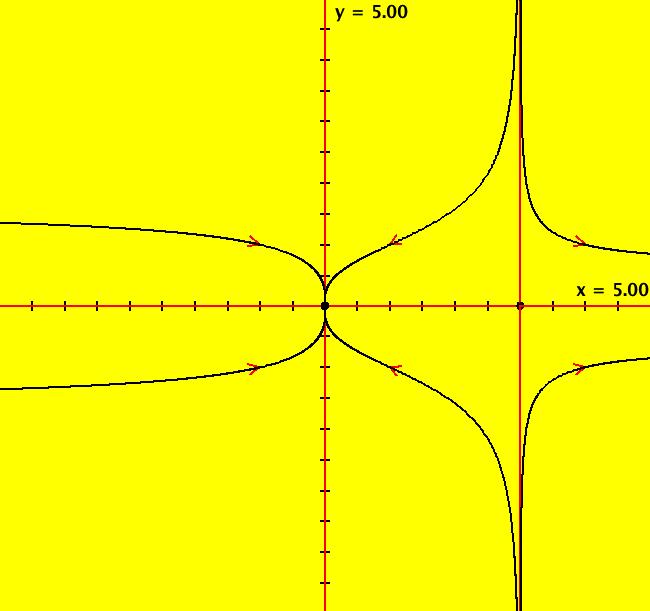
View/Sys/Gal: Ode "2D: 9, poly deg2: (y,-1+x^2+y)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = y, dy/dt = -1+x^2+y. This is a corrected version of example 2.3, p. 11 of MacMath by Hubbard & West. To draw the approximate separatrix system, start trajectories near the fixed points. In this case the fixed points are obviously at (x,y) = (+-1,0) but in general you could just drop 0 = y, 0 = -1+x^2+y into WA to find the fixed points. In WA notation, the Jacobian of the system is D[{y,-1+x^2+y},{{x,y}}] So to find the Jacobian at the (1,0) fixed point, apply WA to evaluate D[{y,-1+x^2+y},{{x,y}}] at x=1, y=0 to get the coefficient array of the linearized system at (1,0) {{0, 1}, {2, 1}} The linearized system at (1,0) is then dx/dt = y, dy/dt = 2*x+y which has eigenvectors and eigenvalues v1 = (1,2), λ1 = 2 v2 = (-1,1), λ2 = -1 Image 1: The R2+ Ode view. Image 2: The EMap view. The prisoner set is just the fixed point at (-1,-1), all other IMap orbits go to infinity.
|
|
|
View/Sys/Gal: Ode "2D: 10, poly deg2: (x*(3-x-2*y),y*(2-x-y))" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = x*(3-x-2*y), dy/dt = y*(2-x-y). The fixed points are at: (0,0), (0,2), (1,i) and (3,0). The Ode separatrix system separates the plane into 7 regions. Image 1: The Ode view. Image 2: The EMap view. All prisoner set orbits go to a fixed point at (2,0).
|
|
|
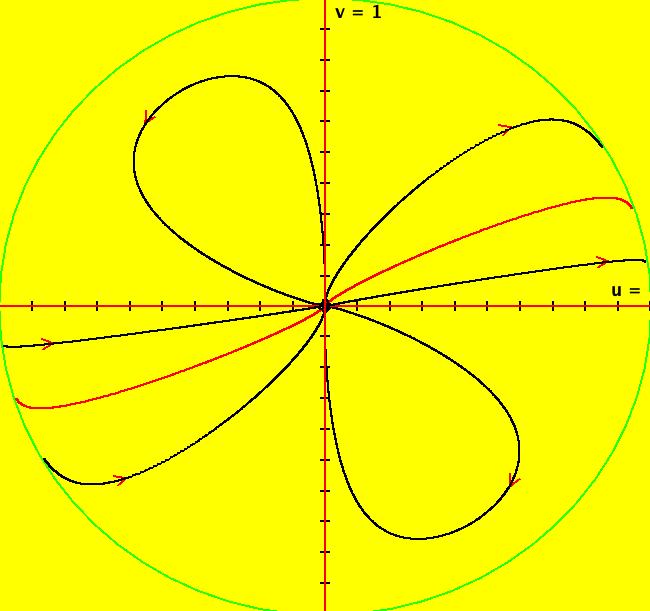
View/Sys/Gal: Ode "2D: 11, poly deg2: (x*(x+y),y*(y/2+x))" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = x*(x+y), dy/dt = y*(y/2+x) The Ode separatrices are the y and x axes and the red curve through (0,0) in 1st and 3rd quadrants. Image 1: The Ode R2+ view. Image 2: the EMap view. All prisoner set orbits go to (0,0), all other orbits go to infinity.
|
|
|
View/Sys/Gal: Ode "2D: 12, poly deg2: (x*(x-3),-y)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = x*(x-3), dy/dt = -y. The 7 separatrices are the 4 vertical line segments and the 3 horizontal line segments emanating from the 2 fixed points. Image 1: The Ode view. Image 2: In the EMap view, all IMap orbits go to infinity.
|
|
|
View/Sys/Gal: Ode "2D: 13, poly deg2: (x^2,-y^2)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = x^2, dy/dt = -y^2 There is a fixed point at (0,0) but the linearized system at (0,0) is just dx/dt = 0, dy/dt = 0 To see this, apply WA to evaluate D[{x^2,-y^2},{{x,y}}] at x=0, y=0 to get {{0, 0}, {0, 0}}. The separatrices are the x and y axes and the line y = -x. They separate the phase space into 6 regions. There are fixed points in R2+ at (u,v) = (0,+-1), (+-1,0), (1/sqrt(2),-1/sqrt(2)) and (-1/sqrt(2),1/sqrt(2)) Image 1: The Ode view. Image 2: The EMap view w/CT 0. The prisoner set is the 2 by 2 square centered at (0,0). All prisoner set orbits go to the fixed point at (0,0).
|
|
|
View/Sys/Gal: Ode "2D: 14, poly deg2 (y,-x+x^2/2)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = y, dy/dt = -x+x^2/2 in the (t,x,y) coordinate system. The 1st order 2D system corresponds to the 2nd order ode y'' = -y+y^2/2 in the (x,y,y') coordinate system. Ode fixed points are at: (0,0) and (2,0). ICs (2,.01) gives Ode separatrices. Image 1: The Ode separatrices. Image 2: The EMap view shows that the prisoner set is a 6 X 6 square centered at (1,1). All prisoner set orbits inside the 6 X 6 square go to (0,0). Orbits on the boundary of the prisoner set do not go to (0,0). Seeds (-2,-2) and (4,-2) go to a fixed point at (4,4). Per-2 orbits at (4,2) and (-2,2) go to (4,0).
|
|
|
View/Sys/Gal: Ode "2D: 15, poly deg2: (y,x+x^2-x*y+a*y), a = -1.00; " in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = y, dy/dt = x+x^2-x*y+a*y in the (t,x,y) coordinate system. The 1st order 2D system corresponds to the 2nd order ode y'' = y+y^2-y*y'+a*y' in the (x,y,y') coordinate system. Parameters are: a = -1.00; The Ode fixed points are at (-1,0) and (0,0). Image 1: The Ode separatrix system. All IMap orbits, except for the orbit with seed (-1,0), which goes to the fixed point (0,0), go to infinity so the IMap separatrix is just the point (-1,0). Image 2: EMap view with seed (-1,0).
|
|
|
View/Sys/Gal: EMap "2D: 16, poly deg2: (y,x+x^2-x*y+a*y), a = -1.00; as EMapCT5" in "SeparatrixExs." This iteration is defined by: x <- y, y <- x+x^2-x*y+a*y. Parameters are: a = -.30; EMap CT: 5 Image 1: An EMap "art image" of the previous system shifted and with a different "a" value.
|
|
|
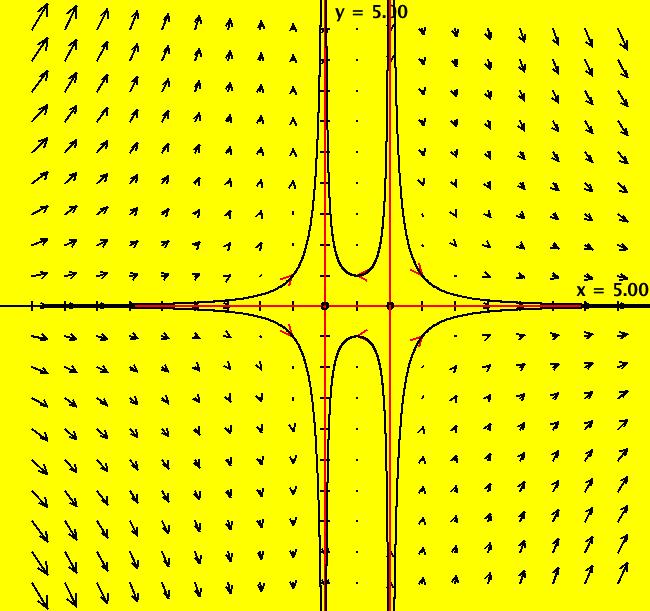
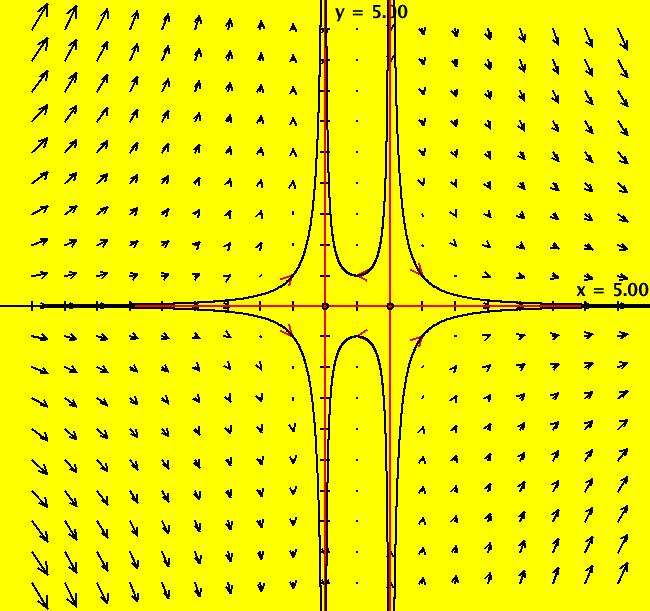
View/Sys/Gal: Ode "2D: 17, poly deg2: (x*(x-1),y*(1-2*x))" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = x*(x-1), dy/dt = y*(1-2*x) The fixed points are at: (x,y) = (0,0), (1,0). The fixed points at infinity are at: (u,v) = (+-1,0), (0,+-1). To draw the separatrices use ICs: (.01,.01), (-.01,-.01) and (1.01,-.01). The separatrices are the straight lines y = 0, x = 0 and x = 1. Image 1: The Ode separatrix system. Image 2: The IMap separatrix system is the boundary of the prisoner set shown in the EMap view. All prisoner set orbits go to (0,0).
|
|
|
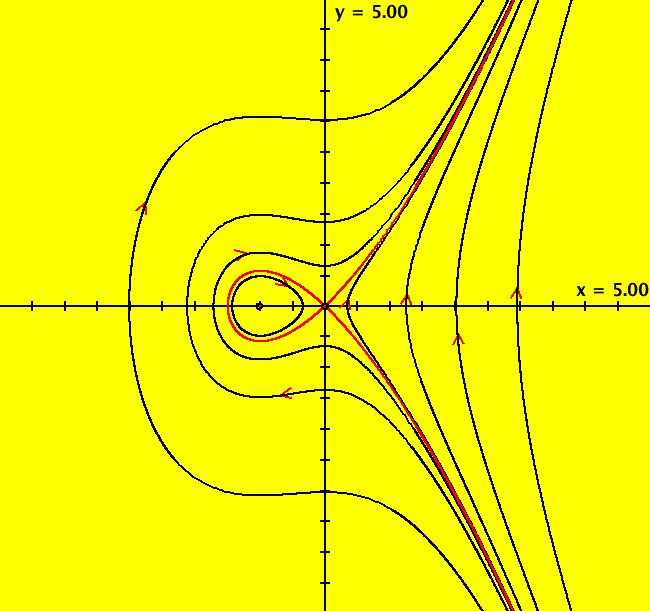
View/Sys/Gal: Ode "2D: 18, poly deg2: AGF version of 2D: 17" in "SeparatrixExs." This AGF version of system "2D: 17"is generated by using the three separatrices of system "2D: 17" as generators: L[1]: y = 0, m = 0, λ = -1 L[2]: x = 0, m = inf, λ = 1 L[3]: (x-1) = 0, m = inf, λ = -1 The degree of the RHS of the system is: 2. The system can also be written as: dx/dt = x*(x-1) dy/dt = y*(1-2*x) The fixed points are at: (x,y) = (0,0), (1,0). The fixed points at infinity are at: (u,v) = (+-1,0), (0,+-1). Image 1: Separatrix system in the Ode view.
|
|
|
View/Sys/Gal: EMap "2D: 19, poly deg2: from H=y^2/2-x^2/2-x^3/3" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = (a*((4*y)/4)), dy/dt = -(a*(-1*((4*x)/4)-(9*x^2)/9)) or dx/dt = a*y, dy/dt = a*x*(x+1). Parameters are: a = 1; Functions are: H=y^2/2-x^2/2-x^3/3 It is a quasiHamiltonian, or generalized Hamiltonian, system. It is a Hamiltonian system iff a = 1. To draw the Ode separatrices, ICs: (+-.001,0) are used. Image 1: The Ode separatrix system. Image 2: The EMap view. The boundary of the 1 by 1 square prisoner set centered at (-.5,-.5) is the IMap separatrix system. All bounded IMap orbits go to (0,0).
|
|
|
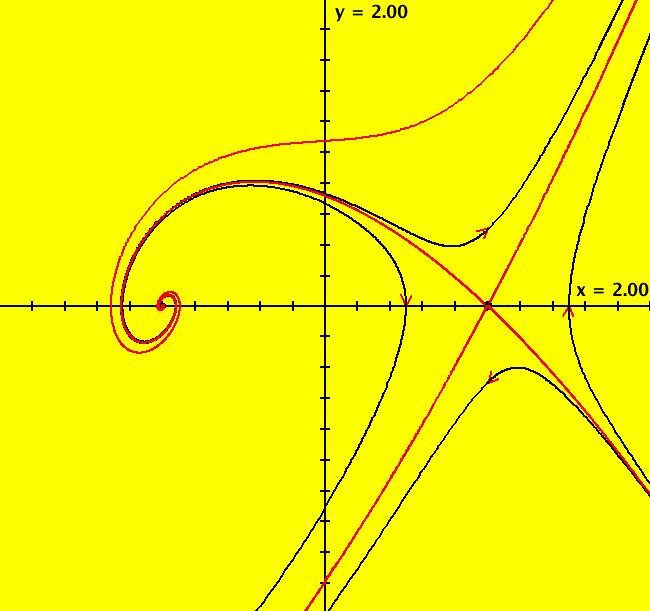
View/Sys/Gal: EMap "2D: 20, poly deg2: from H=y^2/2-x^2/2-x^3/3 as an EMapCT9" in "SeparatrixExs." This iteration is defined by: x <- (a*((4*y)/4)), y <- -(a*(-1*((4*x)/4)-(9*x^2)/9)). Parameters are: a = 2.10; Functions are: H=y^2/2-x^2/2-x^3/3 EMap CT: 9 This is system "2D: 19" shown in the EMap view w/CT 9 using a different "a" value. Image 1: EMap view. Is this a fractal? See the selection square. Image 2: Part of image 1 generated by opening a selection square on the lower right corner of image 1.
|
|
|
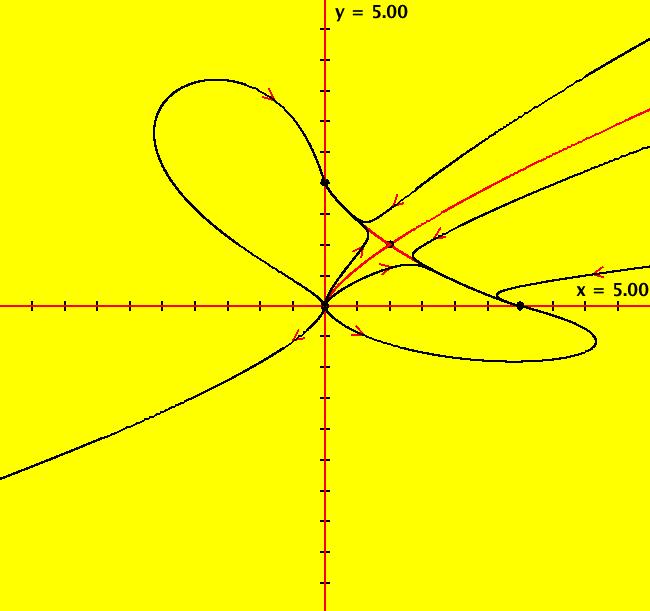
View/Sys/Gal: Ode "2D: 21, poly deg3: (-x+y^2,-y^3+y^2)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = -x+y^2, dy/dt = -y^3+y^2 Fixed points at (x,y) = (0,0), (1,1), y = 0 is a soln. Image 1: The Ode separatrix system. The prisoner set in the EMap view is a strip for -.908 < ~ y < ~ 1.361. All IMap orbits in the prisoner set go to different per-2 limit cycles all of which are on the x axis. Image 2: The IMap view of some per-2 limit cycles. Image 3: The 3D/(t,x) view of the IMap per-2 limit cycles. Image 4: The 3D/(t,y) view of the IMap per-2 limit cycles.
|
|
|
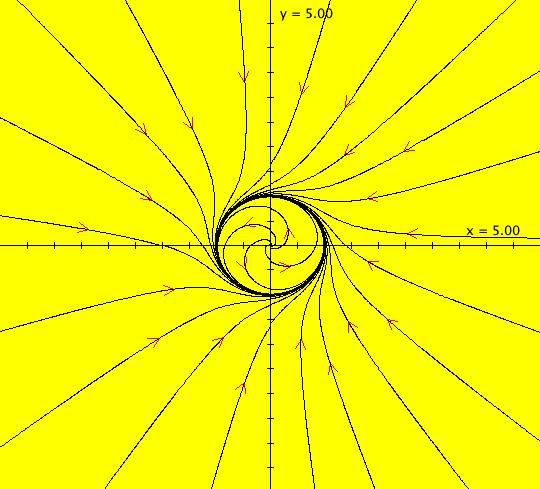
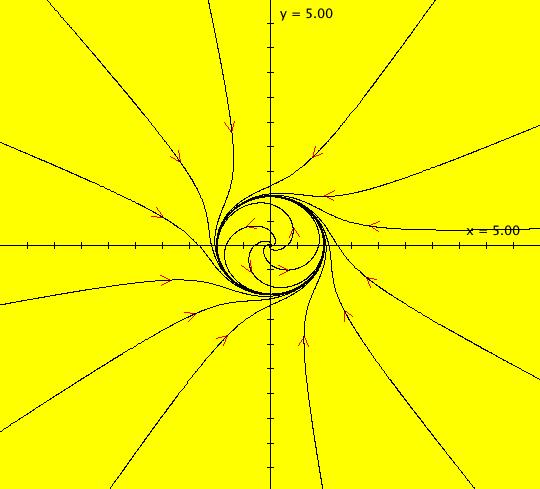
View/Sys/Gal: Ode "2D: 22, nonpoly: ((a*((6*y^2)/4)),-(a*(sin(x))))" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = (a*((6*y^2)/4)), dy/dt = -(a*(sin(x))) Parameters are: a = 1; Functions are: H = y^3/2 - cos(x). This is a Hamiltonian system where H is the Hamiltonian. The solution curves are the level curves of H. The system is generated by OdeFactory by simply entering H in the "user fns:" field. Separatrix ICs: (0,-.001), ( π,.001). The top separatrix is given by H = 1 and the bottom separatrix is given by H = -1. There are cusps at n*pi, n = 0, +-1, +-2,... Use WA to see the level curves of H. Image 1: The separatrix system in the Ode view. The IMap separatrix system is difficult to find. The IMap has fixed points at (0,0) and (1.5,-1) and a per-2 orbit between (0,-1) and (1.5,0). All orbits seem to go to one of the two fixed points or to the period=2 orbit. For example: blue (-2.705521,4.609400) -> (0,0), red (-1.398773,-4.648298) -> (1.5,-1) and green (4.822086,-5.406807) -> per-2. Image 2: The blue, red, green IMap orbits.
|
|
|
View/Sys/Gal: Ode "2D: 23, nonpoly: (sin(pi*x)*cos(pi*y),-cos(pi*x)*sin(pi*y))" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = sin(pi*x)*cos(pi*y), dy/dt = -cos(pi*x)*sin(pi*y) The fixed points are at (+-n,+-n) and the separatrices are the vertical and horizontal lines x = +-n and y = +- n where n is an integer. Image 1: Part of the Ode's infinite separatrix system of 1 by 1 squares. Image 2: The colored vector field. Image 3: The IMap view. All IMap orbits are chaotic and go, in one hop, to: the right sub square, the left sub square or the top and bottom sub squares. The boundaries of the sub squares in the IMap view form the IMap separatrix system.
|
|
|
View/Sys/Gal: Ode "2D: 24, nonauton: (2*(t-1)*y,-2*(t-1)*x)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = 2*(t-1)*y, dy/dt = -2*(t-1)*x This is a nonautonomous system. The trajectories in the phase space are circles but the solution curves in the extended phase space are not periodic functions! The motion on the circles starts ccw, slows down, then reverses goes cw and speeds up. Image 1: The Ode 3D/(t,x,y) view. Image 2: The IMap view. All orbits go to (0,0) in two hops. Both the Ode and the IMap have a fixed point at (0,0) and neither have a separatrix system.
|
|
|
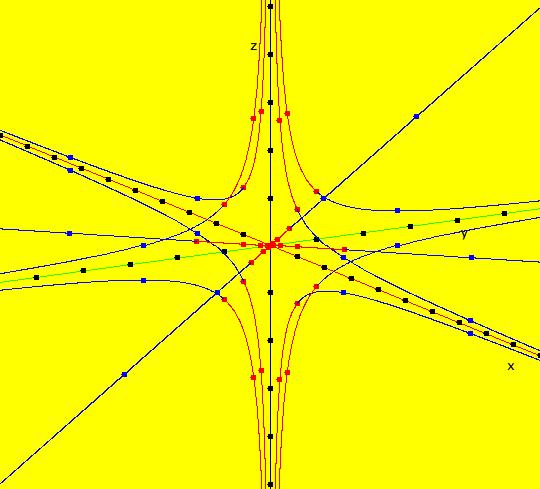
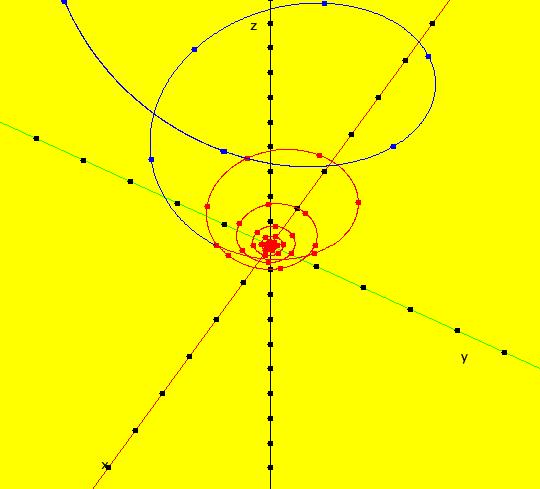
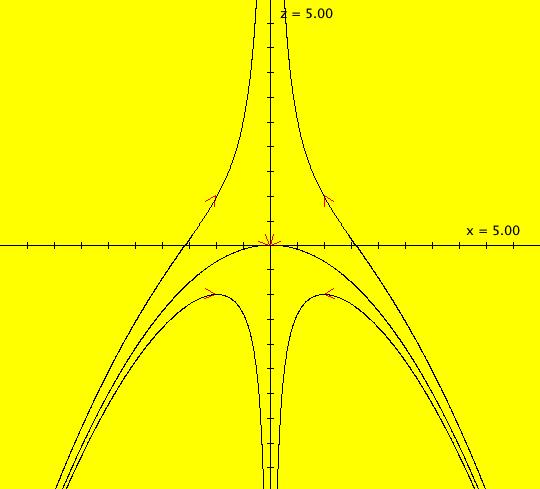
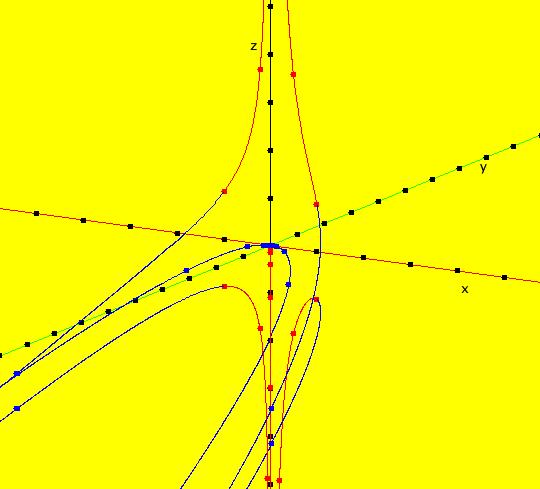
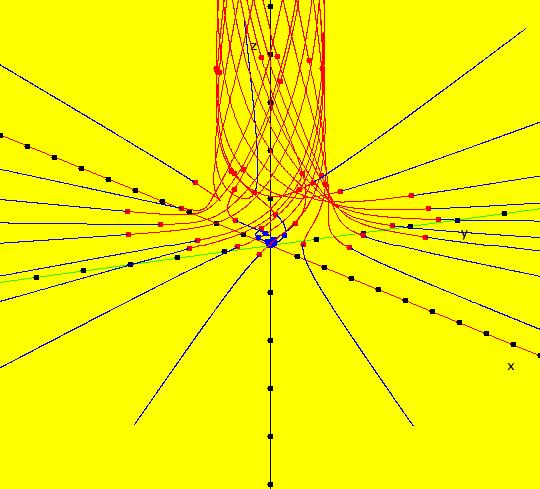
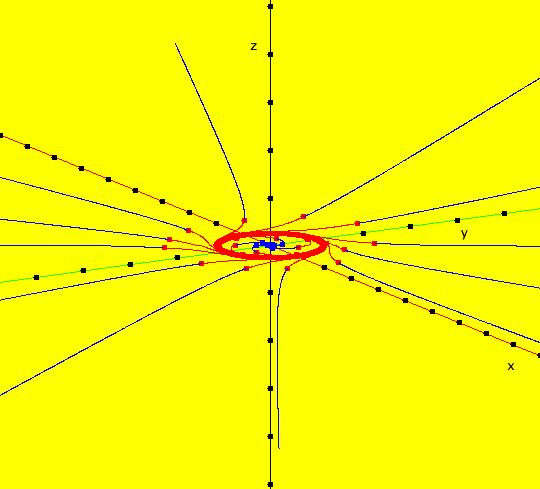
V/S/G: Ode "3D: 1, linear: (-x,-y,z)" in "SeparatrixExs." The trajectories and separatrix systems for nD systems are (n-1)D objects. For 2D systems, the separatrix system is a set of 1D trajectories in the 2D phase space which makes the separatrices easy to envision using a 2D computer display. For n>2, the trajectories and the separatrix systems of nD systems, become much more difficult to envision using a 2D computer display. This system of odes is defined by the equations: dx/dt = -x, dy/dt = -y, dz/dt = z Trajectories for 3D systems reside in the three dimensional phase space (x,y,z). The (x,y), (y,z) and (x,z) views are projections from the phase space onto the three projection planes (x,y,z0), (x0,y,z) and (x,y0,z) respectively. The projection planes are perpendicular to the z, x and y axes. A right handed coordinate system is being used, i.e. if you rotate the +x axis to the +y axis, with your right hand, your thumb will point along the +z axis. In the (x,y) view the +z axis is out of the screen and the 4 trajectories are in the (x,y,0) plane at x = +-1, y = +-1. All trajectories are straight lines in the plane going to the fixed point (0,0,0). Image 1: The z = 0 plane view. In the (y,z) view the +x axis is out of the screen and the 4 trajectories are in the (0,y,z) plane at y = +-1, z = +-1. All trajectories are hyperbolic going to +z or -z. Image 2: The x = 0 plane view. In the (x,z) view, the +y axis is into the screen and the 4 trajectories are in the (x,0,z) plane at x = +-1, z = +-1. All trajectories are hyperbolic going to +z or -z. Image 3: The y = 0 plane view. So, the z = 0 plane, minus the origin, is the separatrix surface. Image 4: The 3D/(x,y,z) view.
|
|
|
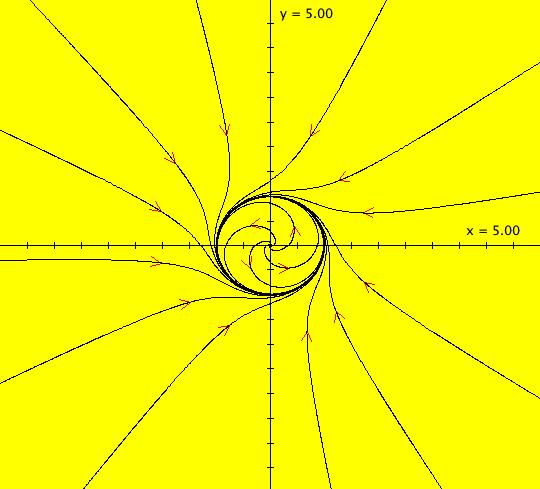
V/S/G: Ode "3D: 2, linear: (-.1*x-y,x-.1*y,-.2*z)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = -.1*x-y, dy/dt = x-.1*y, dz/dt = -.2*z From Perko, p. 56, fig. 4. ICs (x,y,z) = (0,2,3). Image 1: The trajectory projected onto the (x,y) plane. Image 2: The 3D/(x,y,z) view with: Yaw = -30 degrees, Pitch = 60 degrees and Roll = 0 degrees.
|
|
|
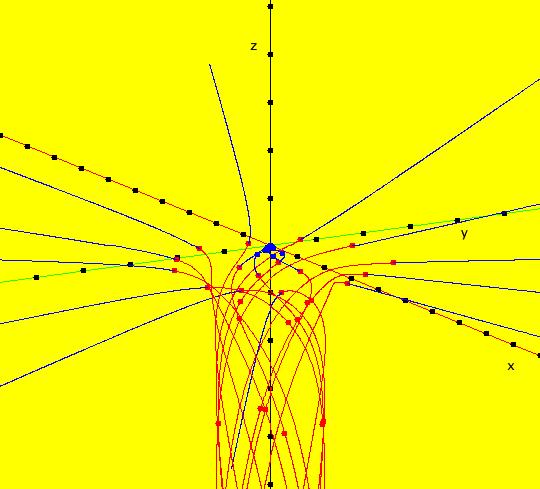
V/S/G: Ode "3D: 3, poly deg2: (-x,-y+x^2,z+x^2)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = -x, dy/dt = -y+x^2, dz/dt = z+x^2 In the y = 0 plane, +y into the screen. Trajectories at x = +-1, z = +-1 and x = +-.001, z = -.001 Image 1: The y = 0 plane. Image 2: The 3D/(x,y,z) view with Yaw = 60, Pitch = 15 and Roll = 0.
|
|
|
V/S/G: Ode "3D: 4, poly deg3: (-y+x*(1-x^2-y^2),x+y*(1-x^2-y^2),z)" in "SeparatrixExs." This system of odes is defined by the equations: dx/dt = -y+x*(1-x^2-y^2), dy/dt = x+y*(1-x^2-y^2), dz/dt = z The only fixed point is at the origin. In the (X,y) view, the +z axis is directly out of the screen and a unit cylinder about the z axis projects onto the (x,y) plane as a unit circle. Image 1: Trajectories started in the z = .5 plane are attracted to the +z half of the unit cylinder in +t. Image 2: The 3D/(x,y,z) view with z = .5 Image 3: Trajectories started in the z = 0 plane stay in the z = 0 plane and are attracted to the unit circle. Image 4: The 3D/(x,y,z) view with z = 0 Image 5: Trajectories started in the z = -.5 plane are attracted to the -z half of the unit cylinder in +t. Image 6: The 3D/(x,y,z) view with z = -.5 The separatrix surface is the unit cylinder about the z axis plus the z plane. The 9 separatrix regions are: inside, outside and on the unit cylinder above and below the z = 0 plane and inside, outside and on the unit circle in the z = 0 plane. Trajectories starting above the z plane wind out of the screen in the +z direction and trajectories starting below the z plane wind into the screen in the -z direction. Trajectories starting in the z = 0 plane, stay in the z = 0.
|
|