Click on an image to go directly to a system or scroll to see the systems in this gallery.

OdeFactory Images and Annotations
An OdeFactory Slide Show Click on a slide to zoom in. Click "video" to see a video.	View/Sys/Gal: Ode " Separatrix Systems for 2D Iteration Maps" in "IMapSeparatrixExs." Range: (vMax,vMin) = (5.000,-5.000), (hMin,hMax) = (-5.000,5.000) VFld: (0) --- Definition of a Separatrix --- A separatrix is defined as something that divides or separates. --- Definition of an Ode Separatrix System --- Classically separatrix systems were defined and studied for Odes. For a 2D system of Odes, the separatrix system is a set of continuous solution curves that partition the phase space into regions containing different topological equivalent solution curves. The separatrix system graphically summarizes all of the dynamical properties of the dynamical system. Reference. --- Finding an Ode Separatrix System --- Ode separatrix curves are generally found by studying trajectories near fixed points. In OdeFactory, the fixed points can be found by selecting "Show Colored Vector Field w/Nullclines." Starting trajectories near the fixed points gives red solution curves that are the separatrices. --- Definition of an IMap Separatrix System --- 2D IMaps generate discrete sequences of points in +t called orbits. Since IMaps do not have continuous solution curves the Ode definition of a separatrix system does not apply to IMaps. Consider this to be a working definition: the separatrix system for an IMap consists of the discrete boundaries of prisoner sets. --- Definition of an IMap Prisoner Set --- A prisoner set is any region of R2 containing a family of topological equivalent IMap orbits. --- Definition of an EMap Prisoner Set --- An EMap prisoner set is defined algorithmically. The defining algorithm depends on two parameters and the shape of the "prison." The two parameters are: the bail out parameter M and the color table size K. M is related to the size of the prison. In OdeFactory, for the EMap view, M = 49 and K = 100. For EMapMax K = 512. Increasing M and/or K gives a more detailed prisoner set but it increases the image rendering time. The prison can be a circle of radius 7 centered at (0,0) or a 14X14 square centered at (0,0). A seed is in the prisoner set if, after the first iteration, it stays inside the prison for at least K iterations. Note that the EMap and IMap definitions of a prison set are different. An EMap prison set is small and centered at the origin whereas an IMap prison set is large. --- Finding an IMap Separatrix System. --- To construct an IMap separatrix system begin by setting the axis parameters in the graphics area to +-7. Next, in the IMap view, and with "Show 2D IMap Orbit Sequence" off, drag to start a several IMap orbits. If the image begins to look like a complicated oriental rug you will need to use the IMap view to find the IMap separatrix system. The separatrix system is generally the boundaries of the KAM islands. If you do not get an oriental rug-like IMap, you should work in the EMapMax view - with a square prison. The separatrix system is the boundaries of the (black) EMapMax prisoner set. --- Miscellaneous --- Prisoner set regions are often distinguished by regions with different kinds of attractors. Attractors include: asymptotic fixed points, asymptotic limit cycles and strange attractors. Other types of prisoner set regions, without attractors, are regions with families of cycles and chaotic regions. It should be noted that in the IMap view, using a square prison, the boundaries of n KAM islands in a KAM island chain form the separatrix of a prisoner set in the EMapMax view. Each orbit in the prisoner set will be periodic with period divisible by n. --- The Systems --- The systems are ordered in this gallery by the increasing complexity of their separatrix systems. A: linear, quadratic B: complex systems: z <- f(z,c) C: non-smooth linear D: 5th deg poly E: non-smooth non-linear
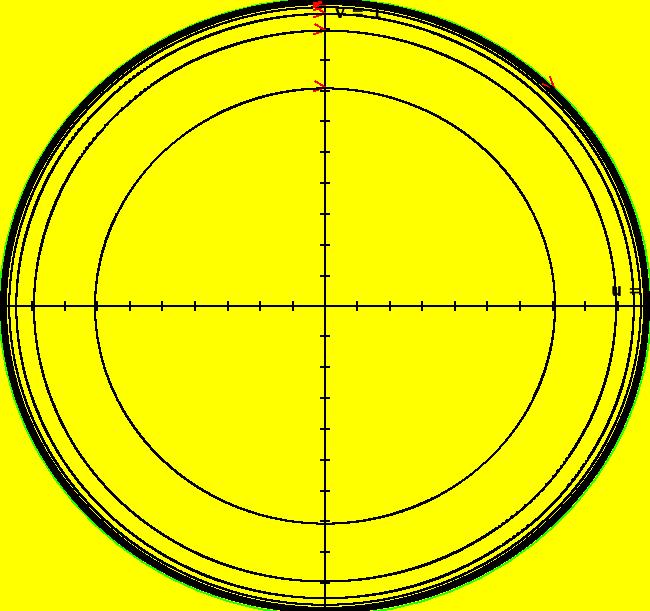
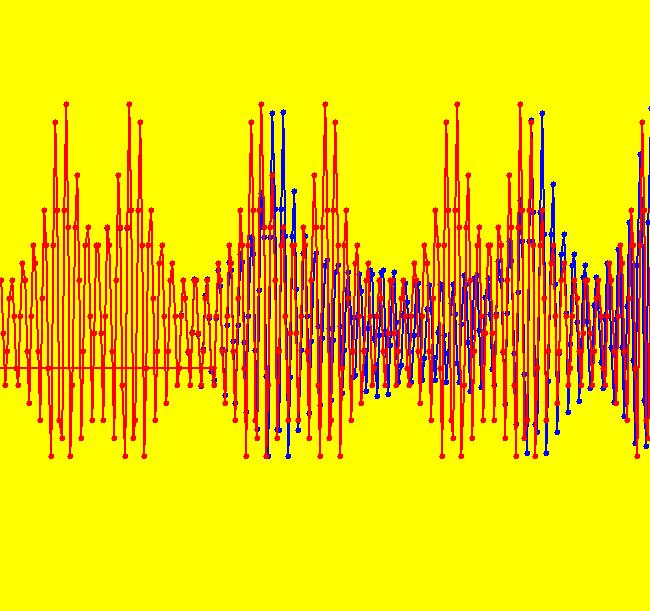
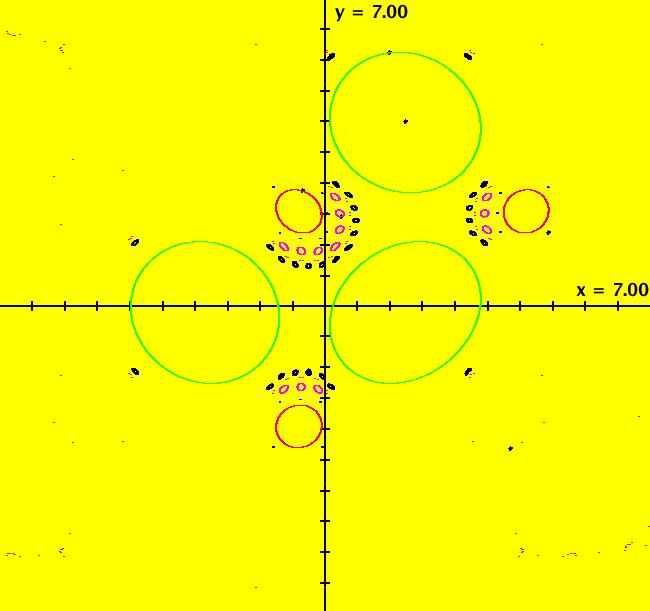
	View/Sys/Gal: EMap "A: linear, EMapMax" in "IMapSeparatrixExs." Range: (vMax,vMin) = (10.000,-10.000), (hMin,hMax) = (-10.000,10.000) VFld: (y,-x) The system is the simple harmonic oscillator (SHO). This iteration is defined by:         x <- y,         y <- -x. EMapMax CT: 0 The separatrix system, for both the IMap and Ode views, is a circle of infinite radius centered at the fixed point (0,0). In the Ode view the trajectories are all circles with period 2 π centered at the fixed point (0,0). Image 1: The Ode trajectories in R2+. In the IMap view, all orbits are squares with period 4 centered at the fixed point (0,0). Image 2: The IMap orbits. Image 3: The EMap for a square prison with seeds at (7,7), (0,8), (2,2) and (0,0). Sometimes the boundary of an EMap prisoner set will be a separatrix for the IMap but that is not the case for this system.
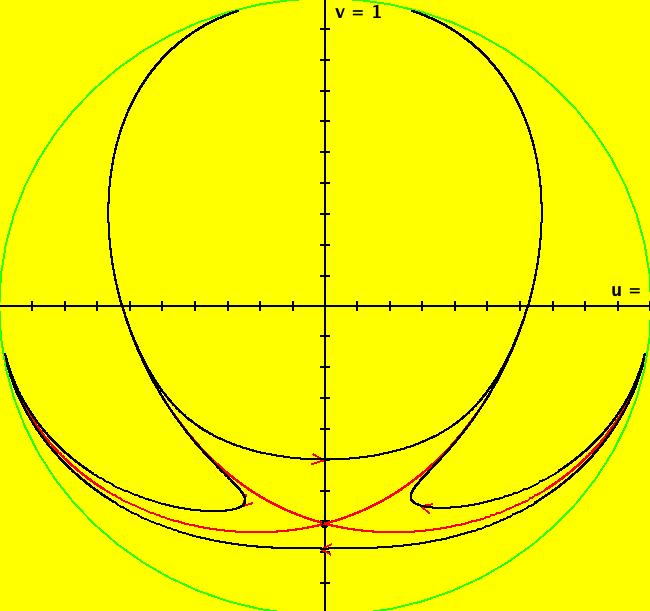
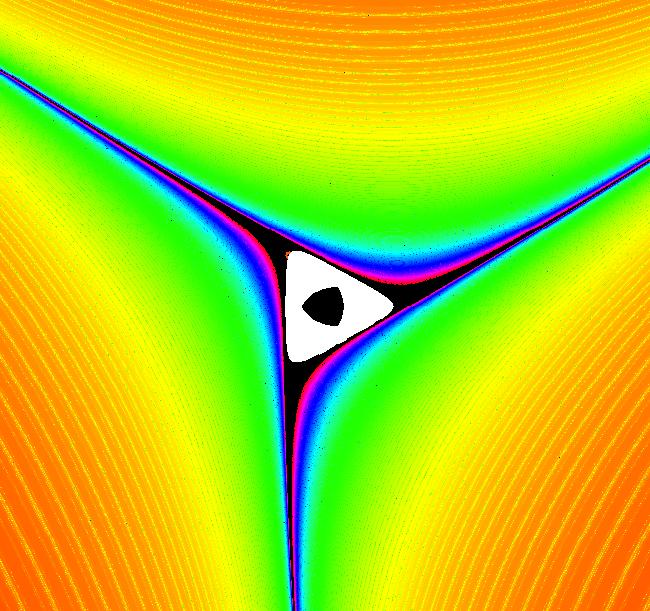
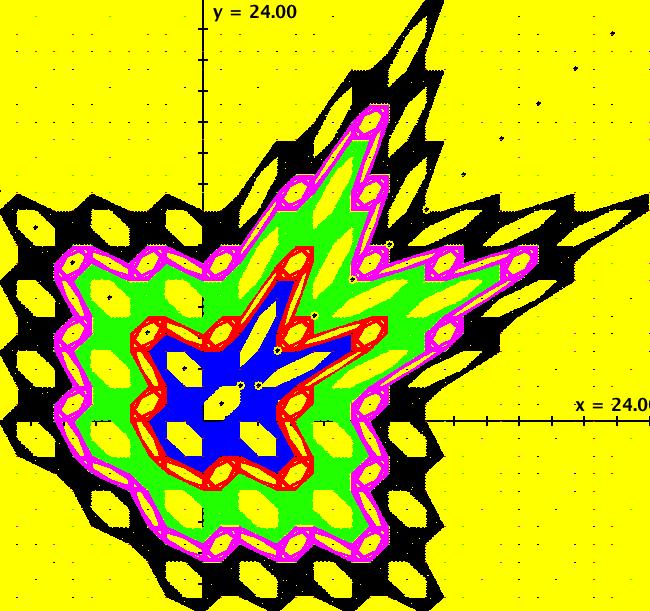
	View/Sys/Gal: EMap "Ab: quadratic, with a strange attractor, EMapMax" in "IMapSeparatrixExs." Range: (vMax,vMin) = (3.500,-3.500), (hMin,hMax) = (-3.500,3.500) VFld: (1+y-a*x^2,b*x), a = 1.4000; b = .3000; This system is called the Henon map. This iteration is defined by:         x <- 1+y-a*x^2,         y <- b*x. Parameters are:         a = 1.4000; b = .3000; EMapMax CT: 0 Image 1: The Ode separatrix system (red curves) in the R2+ view. The fixed point is at (0,-1). Image 2: The IMap view showing a strange attractor (blue curve). For this system you need to use the EMapMax view to find the IMap separatrix system. All orbits starting in the red region go to infinity and all orbits starting in the black region go to the strange attractor. Image 3: The EMapMax view showing the IMap's separatrix system as the border of the EMap's prisoner set. The green dots show the strange attractor after a Flow animation starting at the white dot with the black center.
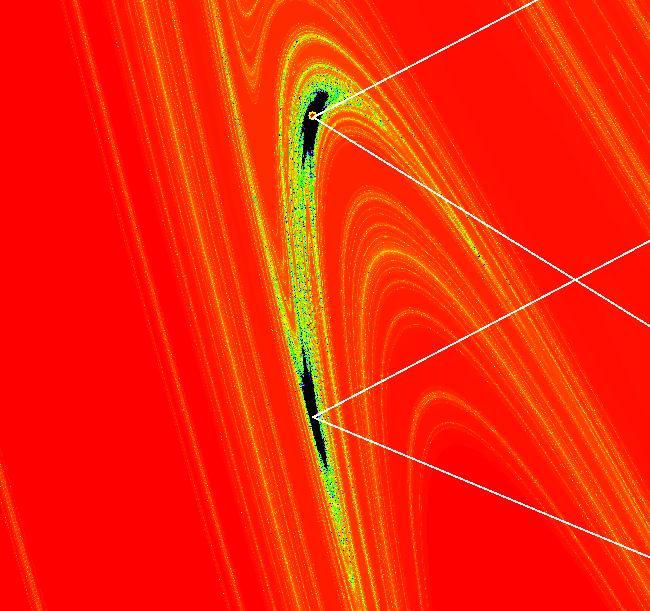
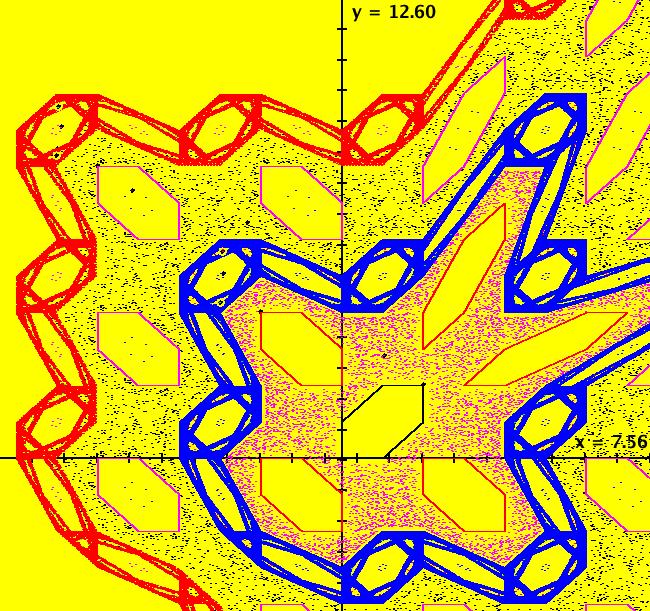
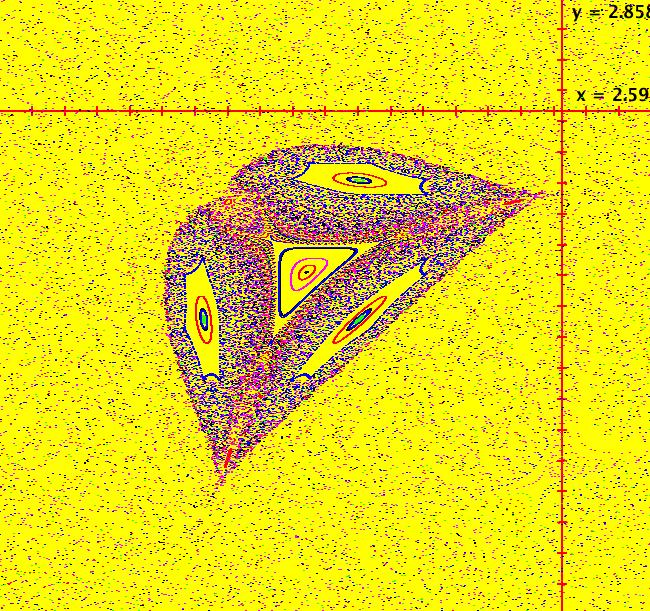
	View/Sys/Gal: EMap "Ac: quadratic, with a very small prisoner set, EMapMax" in "IMapSeparatrixExs." Range: (vMax,vMin) = (0.908,0.363), (hMin,hMax) = (-1.406,-0.891) VFld: (x*cos(a)-(y-x^2)*sin(a),x*sin(a)+(y-x^2)*cos(a)), a = 2.100; This iteration is defined by:         x <- x*cos(a)-(y-x^2)*sin(a),         y <- x*sin(a)+(y-x^2)*cos(a). Parameters are:         a = 2.100; EMapMax CT: 0 This is another system for which you need to use the EMapMax view to find the IMap separatrix system, however, the system has a very small prisoner set. This complicates the search. Image 1: In the EMapMax view the boundary of the inner prisoner set is the outer edge of the white region. The tails of the black regions are not part of the prisoner set. The viewing area is .175 by .175. Image 2: After zooming out 3X (7 by 7 view), we see the outer component of the prisoner set consists of a KAM island ring of 6 islands. There is a per-6 orbit at seed (-1.158468,0.803303). All orbits in the KAM island ring seem to be periodic with periods divisible by 6. Image 3: Zoomed in view of the leftmost pair of KAM islands.
	View/Sys/Gal: EMap "B: z<-z^2+c, c=.25+i*.56, EMapMax" in "IMapSeparatrixExs." Range: (vMax,vMin) = (1.250,-1.250), (hMin,hMax) = (-1.250,1.250) VFld: (x^2-y^2+p,2*x*y+q), p = .2500; q = .5600; This iteration is defined by:         x <- x^2-y^2+p,         y <- 2*x*y+q. Parameters are:         p = .2500; q = .5600; EMapMax CT: 0 Complex IMaps of the form z <- f(z,c) often have compact EMaps with fractal separatrices and attractors that are limit cycles. This is a single connected prisoner set with a fractal boundary and an asymptotic per-4 attractor. Image 1: Shows the per-4 limit cycle attractor.
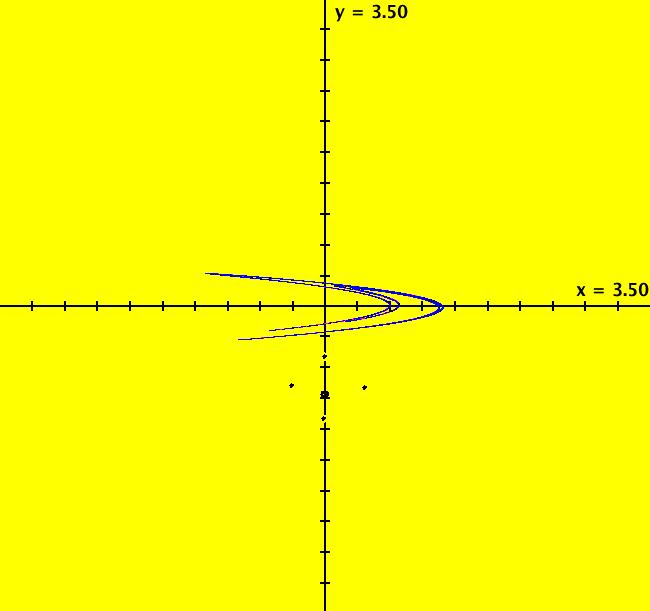
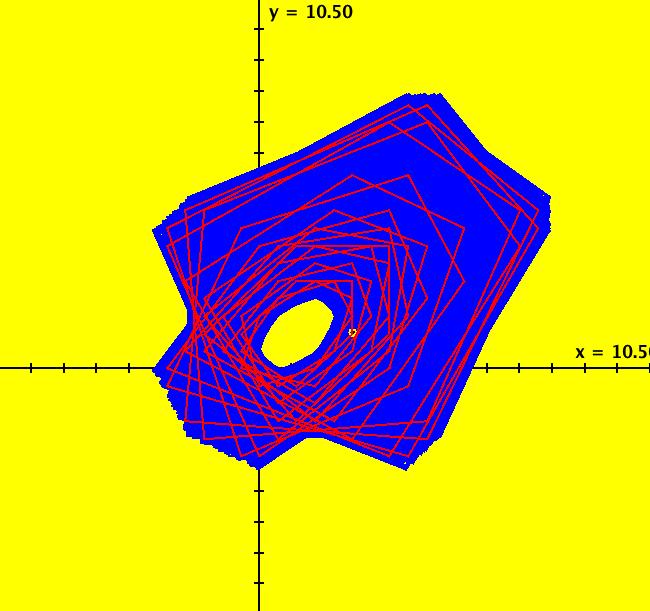
	View/Sys/Gal: EMap "Bb: z <-z^2+c*z, p = .62, q = .78, EMapMax, per-1 and 8" in "IMapSeparatrixExs." Range: (vMax,vMin) = (1.639,-1.639), (hMin,hMax) = (-1.468,1.468) VFld: (p*x-q*y+x^2-y^2,p*x+q*y+2*x*y), p = .6200; q = .7800; This iteration is defined by:         x <- p*x-q*y+x^2-y^2,         y <- p*x+q*y+2*x*y. Parameters are:         p = .6200; q = .7800; EMapMax CT: 0 All orbits either go to infinity or 1-hop to d <= 7 so use the EMapMax view to find the separatrix system. This looks like one connected prisoner set but it is not. The prisoner set is really two different completely disconnected sets with fractal borders, each with an infinite number of segments. Orbits in the elliptically shaped regions go to a fixed point at (0,0), orbits in the 8-petal regions go to a per-8 limit cycle with seed (-0.471361,0.288818). Image 1: The EMapMax view of the per-8 limit cycle and an elliptical segment orbit that goes to the fixed point at (0,0).
	View/Sys/Gal: EMap "Bc: z <- e^z+z*(1-z)+c, c=-1.1+i*.3, EMapMax. per-2 and 7" in "IMapSeparatrixExs." Range: (vMax,vMin) = (2.705,-2.621), (hMin,hMax) = (-0.587,2.356) VFld: (p+x-x^2+y^2+e^x*cos(y),q+y-2*x*y+e^x*sin(y)), p = -1.1000; q = .3100; This iteration is defined by:         x <- p+x-x^2+y^2+e^x*cos(y),         y <- q+y-2*x*y+e^x*sin(y). Parameters are:         p = -1.1000; q = .3100; EMapMax CT: 0 There are 2 basic fractals here: 2-petal and 7-petal spiral fractals. The tails of the 2-petal spirals are 7-petal spirals and vice versa. All orbits in the 2-petal spirals are asymptotic to a per-2 orbit and all orbits in the 7-petal spirals are asymptotic to a per-7 orbit. The seeds are: per-2 seed (0.823383,1.329076), per-7 seed (1.476319,-1.214567). The separatrix system has two parts. One is the border of the 2-petal spirals and the other is the border of the 7-petal spirals. Image 1: The EMapMax view showing the per-2 and per-7 limit cycles.
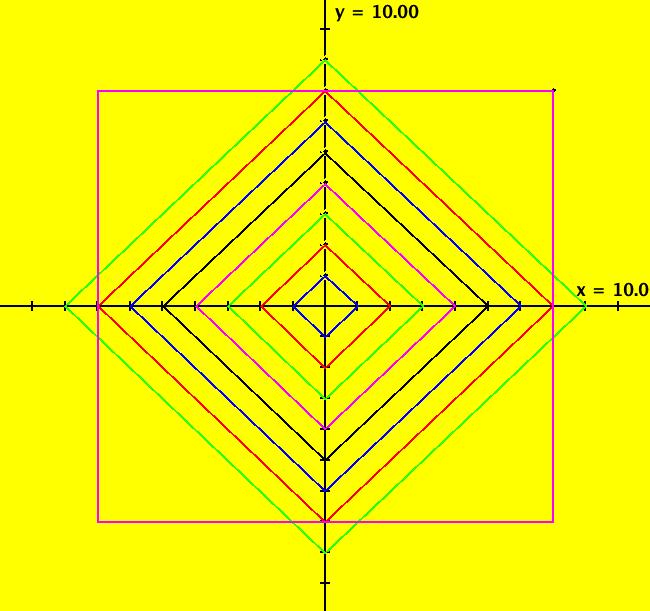
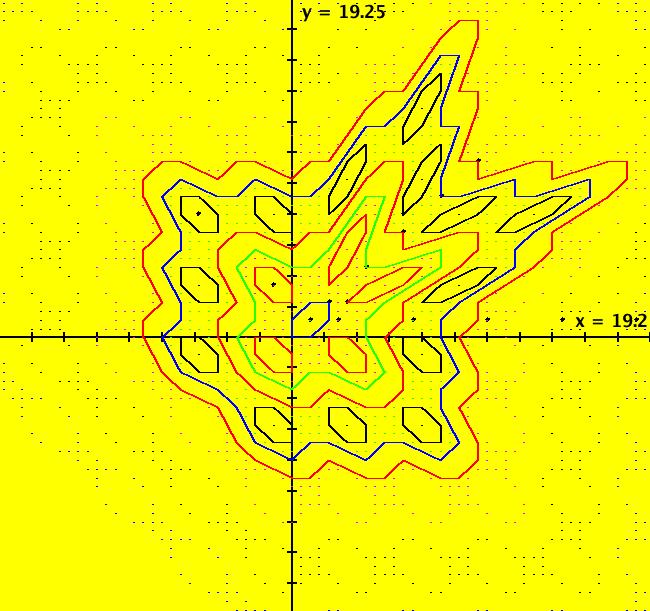
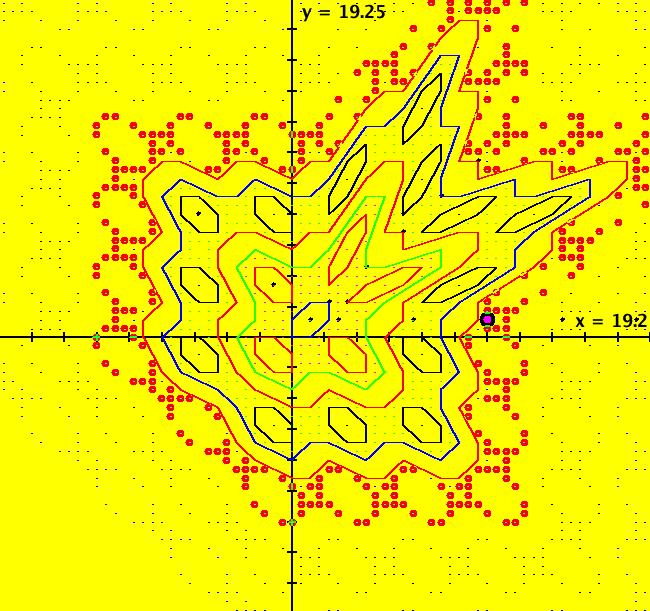
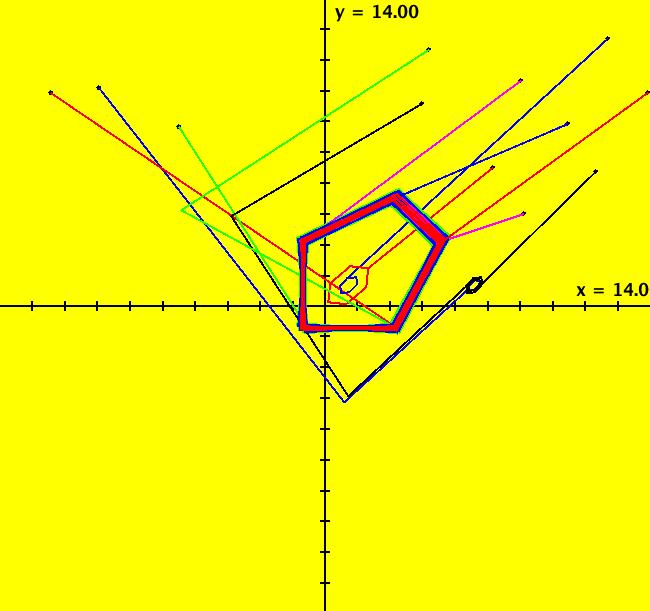
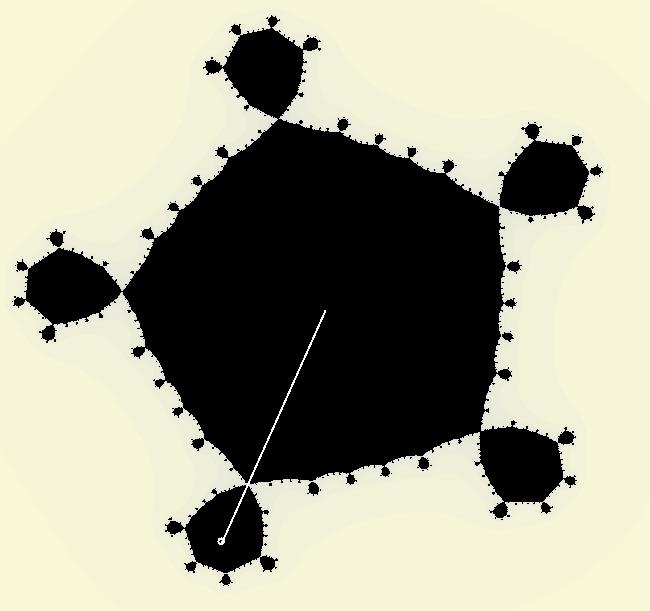
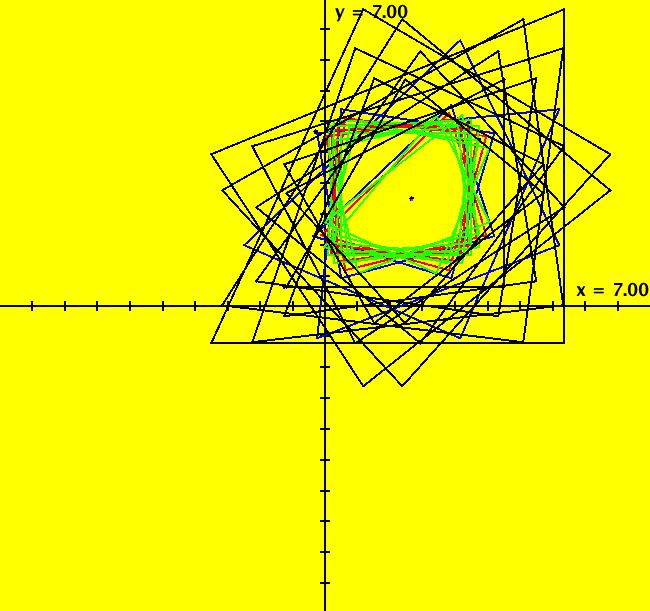
	View/Sys/Gal: IMap "C: linear w/abs, some IMap separatrices" in "IMapSeparatrixExs." Range: (vMax,vMin) = (19.250,-15.750), (hMin,hMax) = (-15.750,19.250) VFld: (1-y+abs(x),x) This iteration is defined by:         x <- 1-y+abs(x),         y <- x. This is the well known gingerbread man map. The system gives "oriental-rug" style IMap images. Orbits are bounded in nested rings that go to infinity. For this system, there are an infinite number of separatrices that can be classified into two different types: (a) ring boundaries - boundaries enclosing chains of islands (the green, red, blue, and red many-sided polygons) that separate adjacent chaotic regions and (b) island boundaries - outer boundaries of individual islands (the hexagon shaped regions) that separate chaotic regions from constant-period regions. The system has one fixed point at (1,1). Orbits starting in the hexagonal islands are periodic. If the orbit starts at the center of the island the period is the number of islands in the ring. For example: (blue) (1,1) gives per-1, (red) (-1,3) gives per-5, (black) (-5,7) gives per-14. For off-center seeds: the blue central hexagonal island contains period 6 orbits, the 5 red hexagonal islands contain period 6*5=30 orbits, the 14 black hexagonal islands contain period 6*14=84 orbits etc. Orbits starting outside of islands are chaotic. Image 1: The solid colored lines form part of the infinite separatrix system for the gingerbread man map. There are three more island chains between the (4.0001,4.0001) green line and the (6.0001,6.0001) red line and three more island chains between the (8.0001,8.0001) blue line and the (10.0001,10.0001) red line. See system Cb for more detail. Separatrix seeds: seed separatrix color (2.0001,2.0001) blue hexagon (2.999,1.999) red hexagons (4.0001,4.0001) green (6.0001,6.0001) red (6.0001,7) black hexagons (8.0001,8.0001) blue (10.0001,10.0001) red Seeds (2,2), (3,2), (4,4), (6,6), (8,8), (6,7), (8,8) and (10,10) give periodic orbits so to highlight the separatrix system, seeds near these points, and a bit inside the chaotic regions, are used. There are isolated periodic/chaotic orbits in chaotic regions: Seed = (2.5+4*n,1), for n = int >= 0, gives a per = 90+162*n orbit. seed n period (2.5,1) 0 90 (6.5,1) 1 252 (10.5,1) 2 414 (14.5,1) 3 576 (18.5,1) 4 738 ... ... ... Seeds very close to (2.5,1) give orbits that diverge from the per-90 orbit so the orbit is both periodic and chaotic. Image 2: The IMap image with seed (2.49999,1) after seed (2.5,1) is added. Image 3: The 3D/(t,x) time-series view for the (2.5,1) and (2.49999,1) orbits with 0 < t < 300. We see that the orbits diverge past t ～ 100. Image 4: The results of a Flow animation for the (10.5,1) per-414 orbit. Aside: If you drop the abs function you get a system with a fixed point at (1,1) and all other orbits are hexagons centered at (1,1). The separatrix system, and all of the interesting structure, essentially goes away!
	View/Sys/Gal: IMap "Cb: linear w/abs, even ring IMap detail" in "IMapSeparatrixExs." Range: (vMax,vMin) = (12.605,-4.277), (hMin,hMax) = (-8.415,7.560) VFld: (1-y+abs(x),x) This iteration is defined by:         x <- 1-y+abs(x),         y <- x. This is part of the 1st, 2nd, 3rd and 4th rings out from the center in system C. All even numbered rings have the same structure. The 3rd ring contains the magenta hexagons. The black dust around the magenta hexagons shows the first 10,000 steps of a chaotic orbit in the chaotic region between the red and blue rings. The 14 magenta islands contain per=84=6*14 orbits. The red, black and blue regions are chaotic and separate. For yellow regions in the red ring:         outer subring has per=291=3*97 orbits,         central subring has per=222=6*37 orbits,         inner subring has per=264=6*44 orbits. For yellow regions in the blue ring:         outer subring has per=156=6*26 orbits,         central subring has per=114=6*19 orbits,         inner subring has per=129=3*43 orbits. The boundaries of the yellow regions in the red and blue rings are separatrices. Image 1: The first two even numbered gingerbread man rings (red and blue) each with three island chains.
	View/Sys/Gal: IMap "Cc: linear w/abs, larger IMap" in "IMapSeparatrixExs." Range: (vMax,vMin) = (24.000,-11.000), (hMin,hMax) = (500.000,1500.000) VFld: (1-y+abs(x),x) This iteration is defined by:         x <- 1-y+abs(x),         y <- x. Here the inner gingerbread ring is colored blue. Image 1: The ring-like pattern of this image, not all of which is shown, extends out to infinity. All of the IMap orbits are bounded. Orbits in the filled in regions are chaotic. As was noted in system C, each filled-in region has one periodic orbit which is also chaotic. The boundaries of the different colored rings in the IMap view are separatrices between the regions that contain chaotic orbits and regions that contain periodic orbits. System Cb shows the (red) 2nd ring region in more detail. The following table contains seeds at (x,-x+2) for n an integer >= 0. These are seeds at the centers of the hexagons. For x=-1-4*n, per = -9/4*x+5-9/4 = 9*n+5 For x=-3-4*n, per = -18/4*x+19-3*18/4 = 18*n+19 n period center seed 0 5 (-1,3) 0 19 (-3,5) 1 14 (-5,7) 1 37 (-7,9) 2 23 (-9,11) 2 55 (-11,13) 3 32 (-13,15) 3 73 (-15,17) 4 41 (-17,19) 4 91 (-19,21) 5 50 (-21,23) ... ... ... 100 905 (-401,403) 101 1819 (-403,405) For off-center seeds the periods are larger by a factor of 6. For example, seed (-21.1,23) gives a period 300 orbit as does seed (-21,22.9). All off-center seeds in hexagons in the same ring have the same period. In this next table the seeds are at (x,x) and the periods are related to x as follows: x = 2+4*n gives per = 27/4*x-7.5 = 27*n+6, and x = 4+4*n gives per = 27/4*x-3 = 27*n+24, for n is an integer >= 0. The period is the number of islands in the ring. The outer boundaries of the chaotic regions are periodic orbits with seeds (x,x). The (2,2) and (4,4) orbits bound the blue chaotic region. The (4,4) and (6,6) orbits bound the red chaotic region, etc. n period seed 0 6 (2,2) 0 24 (4,4) 1 33 (6,6) 1 51 (8,8) 2 60 (10,10) 2 78 (12,12) 3 87 (14.14) 3 105 (16,16) 4 114 (18,18) 4 132 (20,20) 5 141 (22,22) 5 159 (24,24) 6 168 (26,26) 6 186 (28,28) 7 195 (30,30) 7 213 (32,32) 8 222 (34,34) 8 654 (98,98) 49 1347 (200,200) 99 2697 (400,400) 199 5397 (800,800) 249 6747 (1000,1000) ... ... ... The even numbered rings contain large islands surrounded by several smaller islands. You need to zoom in on part of the red ring to see the smaller islands (see system Cb). For this system the prisoner set in the EMapMax view is too small to show the full separatrix system. The complete separatrix system consists of the outer borders of the rings and the inner borders of the yellow islands inside the rings. The color filled regions contain chaotic orbits. To check that an orbit in a color filled region is chaotic, start a nearby orbit then open orbit editors on the pair of orbits and you will see that their endpoints are much different. Image 2: The 3D/(x,t) view, for 500 <= t <= 1500, of two orbits in the black ring starting .000002 from each other.
	View/Sys/Gal: EMap "Cd: linear w/abs & %a, a = 1.5, EMapMax" in "IMapSeparatrixExs." Range: (vMax,vMin) = (7.000,-7.000), (hMin,hMax) = (-7.000,7.000) VFld: (1-y+abs(x),x%a), a = 1.50; This iteration is defined by:         x <- 1-y+abs(x),         y <- x%a. Parameters are:         a = 1.50; EMapMax CT: 0 This is a variation of the gingerbread man map where "%" is the Java mod operator. For small |a|, x%a ≠ x but as parameter "a" get large, x%a -> x so this system becomes the gingerbread man map. For a = 1.5 we again get an infinite IMap but in this case the IMap is sparse. The EMapMax view shows that the separatrix system for a = 1.5 is very different than the separatrix system for system C:. The boundaries of the prisoner-set (black regions) form the system Cd: separatrix system. Image 1: All prisoner-set orbits go to hexagons (in at most three steps) in the first four hexagons, up from the bottom, on the right.
	View/Sys/Gal: IMap "Ce: linear w/abs & %a, a = 5.4, EMapMax" in "IMapSeparatrixExs." Range: (vMax,vMin) = (14.000,-14.000), (hMin,hMax) = (-14.000,14.000) VFld: (1-y+abs(x),x%a), a = 5.4000; This iteration is defined by:         x <- 1-y+abs(x),         y <- x%a. Parameters are:         a = 5.4000; EMapMax CT: 0 For the best image, the square prison is being used. We see that this system is morphing into the gingerbread man map. Image 1: The EMapMax view with several prisoner set orbits. Image 2: The IMap view also shows where the orbits with seeds in the prisoner sets end up.
	View/Sys/Gal: EMap "D: quintic poly, p = .54, q = 1, EMapMax per-13" in "IMapSeparatrixExs." Range: (vMax,vMin) = (1.700,-1.700), (hMin,hMax) = (-1.700,1.700) VFld: (y*(5*x^4-10*x^2*y^2+y^4)/4+p,-x*(x^4-10*x^2*y^2+5*y^4)/4+q), p = .5400; q = 1.0000; This iteration is defined by:         x <- y*(5*x^4-10*x^2*y^2+y^4)/4+p,         y <- -x*(x^4-10*x^2*y^2+5*y^4)/4+q. Parameters are:         p = .5400; q = 1.0000; EMapMax CT: 0 Orbits -> ∞ or stay near (0,0) so the EMapMax view is used. Image 1: A single connected 13-petal fractal prisoner set where the attractor is a per-13 limit cycle. The separatrix system is the fractal boundary of the prisoner set.
	View/Sys/Gal: EMap "Db: quintic poly, p = .54, q = 1.1, EMap per-2" in "IMapSeparatrixExs." Range: (vMax,vMin) = (1.700,-1.700), (hMin,hMax) = (-1.700,1.700) VFld: (y*(5*x^4-10*x^2*y^2+y^4)/4+p,-x*(x^4-10*x^2*y^2+5*y^4)/4+q), p = .5400; q = 1.1000; This iteration is defined by:         x <- y*(5*x^4-10*x^2*y^2+y^4)/4+p,         y <- -x*(x^4-10*x^2*y^2+5*y^4)/4+q. Parameters are:         p = .5400; q = 1.1000; EMapMax CT: 0 Orbits -> ∞ or stay near (0,0) so the EMapMax view is used. Image 1: A single connected 2-petal fractal prisoner set showing the per-2 limit cycle attractor. Image 2: Orbits going to the attractor. The separatrix system is the fractal boundary of the prisoner set.
	View/Sys/Gal: EMap "Dc: quintic poly, p = -.54, q = -1.3, EMapCT10 per-2" in "IMapSeparatrixExs." Range: (vMax,vMin) = (1.700,-1.700), (hMin,hMax) = (-1.700,1.700) VFld: (y*(5*x^4-10*x^2*y^2+y^4)/4+p,-x*(x^4-10*x^2*y^2+5*y^4)/4+q), p = -.5400; q = -1.3000; This iteration is defined by:         x <- y*(5*x^4-10*x^2*y^2+y^4)/4+p,         y <- -x*(x^4-10*x^2*y^2+5*y^4)/4+q. Parameters are:         p = -.5400; q = -1.3000; EMap CT: 10 The four IMap systems with: p q -0.54 -1.3 .54 1.3 1.3 -.54 -1.3 .54 have a per-2 attractor at seed (x,y) = (p,q). Image 1: The per-2 attractor for this (p,q) = (-.54,-1.3) system.
	View/Sys/Gal: EMap "Dd: Dc's bifurcation diagram EMap" in "IMapSeparatrixExs." Range: (vMax,vMin) = (1.700,-1.700), (hMin,hMax) = (-1.700,1.700) VFld: (x,y,w*(5*z^4-10*z^2*w^2+w^4)/4+x,-z*(z^4-10*z^2*w^2+5*w^4)/4+y) This system of odes is defined by the equations:         dx/dt = x,         dy/dt = y,         dz/dt = w*(5*z^4-10*z^2*w^2+w^4)/4+x,         dw/dt = -z*(z^4-10*z^2*w^2+5*w^4)/4+y. This is the analog of the Mandelbrot set for system Dc in the "(p,q)" plain. The (p,q) values that give the per-2 attractors discussed for system Dc are in the four large nodes at (x,y) = "(p,q)" = (.54,1.3) etc. Image 1: The "(p,q)" value (.54,1.3) is the white dot in this EMap image of Dc's bifurcation diagram.
	View/Sys/Gal: EMap "E: sgn, sqrt, and abs, EMapMax per-7, 25, 29, 33, 37" in "IMapSeparatrixExs." Range: (vMax,vMin) = (2.859,1.634), (hMin,hMax) = (1.439,2.598) VFld: (y-sgn(x)*sqrt(abs(b*x-c)),a-x), a = 4.300; b = .710; c = 1.300; This iteration is defined by:         x <- y-sgn(x)*sqrt(abs(b*x-c)),         y <- a-x. Parameters are:         a = 4.300; b = .710; c = 1.300; EMapMax CT: 0 Starting many orbits in the IMap view gives an oriental rug type image so the separatrix system is very complicated. Image 1: IMap view of "oriental rug." The EMapMax view, using a square prison seems to indicate that all orbits -> ∞ or stay near (0,0) but this is not the case. This system has per-7, 25, 29, 33, 37, ... distinct prisoner sets. Image 2: EMapMax view showing the per-7 prisoner set using a square prison. Image 3: The IMap zoomed in on the central part of the EMap shows a per-3n prisoner set (the two eyes and the mouth) and per-n prisoner set (the nose) with chaotic boundaries. period seed 7 (5.281783,2.932635 25 (3.209902,4.199363) 29 (3.262419,4.107199) 33 (3.142562,4.107560) 37 (2.889756,4.228904) ... ...
	View/Sys/Gal: EMap "Eb: sgn, sqrt, and abs, IMap" in "IMapSeparatrixExs." Range: (vMax,vMin) = (7.000,-7.000), (hMin,hMax) = (-7.000,7.000) VFld: (y-sgn(x)*sqrt(abs(b*x-c)),a-x), a = 1.6000; b = .5800; c = -5.0000; This iteration is defined by:         x <- y-sgn(x)*sqrt(abs(b*x-c)),         y <- a-x. Parameters are:         a = 1.6000; b = .5800; c = -5.0000; Orbits in the green and red regions have period 3n where n is an integer > 0. Image 1: The IMap view with:         2, 3n separatrix regions, green and red,         1 29n separatrix region, black,         1 13n separatrix region, magenta,         1 17n separatrix region, blue. For this choice of parameters the orbits -> ∞ or stay near (0,0) so we could try the EMapMax view. Image 2: The EMapMax view using a square prison. The 3 largest black regions are the 3 green IMap regions and next largest black regions are the 3 red IMap regions. The per-3 orbit shown is at (1.735412,4.186236).
	View/Sys/Gal: IMap "Ec: sgn, sqrt, and abs, c = 1, EMapMax per-1, 14, 19, 34, 42" in "IMapSeparatrixExs." Range: (vMax,vMin) = (7.000,-7.000), (hMin,hMax) = (-7.000,7.000) VFld: (y-sgn(x)*sqrt(abs(b*x-c)),a-x), a = 4.3000; b = .7100; c = 1.0000; This iteration is defined by:         x <- y-sgn(x)*sqrt(abs(b*x-c)),         y <- a-x. Parameters are:         a = 4.3000; b = .7100; c = 1.0000; EMapMax CT: 0 Use the square prison. There are disjoint prisoner sets. There are several periodic orbits but they are not limit cycles. period seed color 1 (1.865251,2.434749)) black dot 14 (2.899165,6.053510) blue 19 (3.265536,4.024739) red 34 (3.521330,3.598579) green 42 (-0.863615,0.452369) black Image 1: EMapMax view shows the per-42 prisoner set using the square prison. Image 2: The IMap view with some periodic orbits. This system gives an oriental rug IMap image so the EMap view only gives limited information about the separatrix system. Image 3: Oriental rug in the IMap view.